From Mechanics
(Difference between revisions)
|
|
| Line 44: |
Line 44: |
| | | [[Image:test3ans1.gif]] | | | [[Image:test3ans1.gif]] |
| | | | |
| - | | (3 marks) | + | | (1 marks) |
| | | | |
| | | | |
| Line 51: |
Line 51: |
| | | T = 4900 N | | | T = 4900 N |
| | | | |
| - | | (3 marks) | + | | (1 marks) |
| | | | |
| | | | |
| Line 61: |
Line 61: |
| | \end{align}</math> | | \end{align}</math> |
| | | | |
| - | | (1 mark) | + | | (3 mark) |
| | | | |
| | + | |- |
| | + | | 3 (d) |
| | + | | <math>\begin{align} |
| | + | & 4800-4900=500a \\ |
| | + | & a=\frac{-100}{500}=-0.2\text{ m}{{\text{s}}^{\text{-2}}} \\ |
| | + | & 0.\text{2 m}{{\text{s}}^{-\text{2}}}\quad \text{downwards} \\ |
| | + | \end{align}</math> |
| | + | |
| | + | | (4 mark) |
| | | | |
| | |- | | |- |
| | | | | | |
| | | | | | |
| - | | '''(7 marks)''' | + | | '''(9 marks)''' |
| | | | |
| | | | |
Revision as of 09:09, 8 April 2012
Solutions
| 1 (a)
| \displaystyle \begin{align}
& 0=24.5-9.8t \\
& t=\frac{24.5}{9.8}=2.5\text{ seconds} \\
\end{align}
| (3 marks)
|
| 1 (b)
| \displaystyle \begin{align}
& {{0}^{2}}={{24.5}^{2}}+2\times (-9.8)\times s \\
& s=\frac{{{24.5}^{2}}}{2\times 9.8}=30.625\text{ m} \\
\end{align}
OR
\displaystyle s=\frac{1}{2}(24.5+0)\times 2.5=30.625\text{ m}
| (3 marks)
|
| 1 (c)
| 61.25 m
| (1 marks)
|
|
|
| (7 marks)
|
| 2 (a)
| 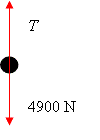
| (1 marks)
|
| 2 (b)
| T = 4900 N
| (1 marks)
|
| 2 (c)
| \displaystyle \begin{align}
& T-4900=500\times 0.6 \\
& T=300+4900=5200\text{ N} \\
\end{align}
| (3 mark)
|
| 3 (d)
| \displaystyle \begin{align}
& 4800-4900=500a \\
& a=\frac{-100}{500}=-0.2\text{ m}{{\text{s}}^{\text{-2}}} \\
& 0.\text{2 m}{{\text{s}}^{-\text{2}}}\quad \text{downwards} \\
\end{align}
| (4 mark)
|
|
|
| (9 marks)
|
| 3 (a)
| 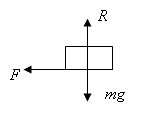
| (1 mark)
|
| 3 (b)
| \displaystyle F=2\times 1\textrm{.}8=3\textrm{.}6\text{ N}
| (2 marks)
|
| 3 (c)
| \displaystyle R=2\times 9\textrm{.}8=19\textrm{.}6\text{ N}
| (2 marks)
|
| 3 (d)
| \displaystyle \begin{align}
& 4800-4900=500a \\
& a=\frac{-100}{500}=-0.2\text{ m}{{\text{s}}^{\text{-2}}} \\
& 0.\text{2 m}{{\text{s}}^{-\text{2}}}\quad \text{downwards} \\
\end{align}
| (3 marks)
|
|
|
| (8 marks)
|
| 4 (a)
| 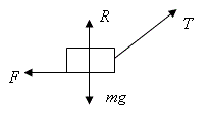
| (1 mark)
|
| 4 (b)
| \displaystyle \begin{align}
& R+T\sin 30{}^\circ =200\times 9 \textrm{.}8 \\
& R+0 \textrm{.}5T=1960 \\
& R=1960-0 \textrm{.}5T \\
\end{align}
| (3 marks)
|
| 4 (c)
| \displaystyle
\displaystyle \begin{align}
& F=T\cos 30{}^\circ \\
& T\cos 30{}^\circ =0\textrm{.}6(1960-0\textrm{.}5T) \\
& T(\cos 30{}^\circ +0\textrm{.}3)=1176 \\
& T=\frac{1176}{(\cos 30{}^\circ +0\textrm{.}3)}=1010\text{ N} \\
\end{align}
| (4 marks)
|
|
|
| (8 marks)
|
| 5 (a)
| \displaystyle \begin{align}
& 5\mathbf{i}-2\mathbf{j}=4\mathbf{i}+3\mathbf{j}+10\mathbf{a} \\
& \mathbf{a}=\frac{1}{10}(\mathbf{i}-5\mathbf{j})=\left( 0\textrm{.}1\mathbf{i}-0\textrm{.}5\mathbf{j} \right)\text{ m}{{\text{s}}^{\text{-2}}} \\
\end{align}
AG
| (3 marks)
|
| 5 (b)
| \displaystyle \mathbf{r}=(4\mathbf{i}+3\mathbf{j})t+0\textrm{.}5(0\textrm{.}1\mathbf{i}-0\textrm{.}5\mathbf{j}){{t}^{2}}
| (2 marks)
|
| 5 (c)
| \displaystyle \begin{align}
& \mathbf{r}=(4t+0\textrm{.}05{{t}^{2}})\mathbf{i}+(3t-0\textrm{.}25{{t}^{2}})\mathbf{j} \\
& 3t-0\textrm{.}25{{t}^{2}}=0 \\
& t(3-0\textrm{.}25t)=0 \\
& t=0\text{ or }t=\frac{3}{0\textrm{.}25}=12\text{ s} \\
& t=12\text{ s} \\
\end{align}
| (3 marks)
|
| 5 (d)
| \displaystyle \begin{align}
& \mathbf{v}=(4+0\textrm{.}1t)\mathbf{i}+(3-0\textrm{.}5t)\mathbf{j} \\
& 3-0\textrm{.}5t=0 \\
& t=6 \text{ s} \\
\end{align}
| (3 marks)
|
|
|
| (11 marks)
|
AG: Answer Given in Question – Working must justify answer.



