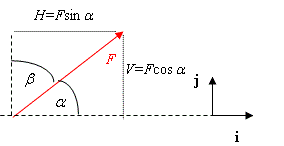From Mechanics

Theory

Exercises

Key Points

The force \displaystyle \mathbf{F} can be resolved into components as follows.

\displaystyle \begin{align} & \mathbf{F}=F\cos \alpha \mathbf{i}+F\cos (90-\alpha )\mathbf{j} \\ & =F\cos \alpha \mathbf{i}+F\sin \alpha \mathbf{j} \end{align}

\displaystyle F is the magnitude of the force.

\displaystyle F\cos \alpha is one component of the force. If \displaystyle \mathbf{i} is horizontal, \displaystyle F\cos \alpha is called the horizontal component of the force.

\displaystyle F\sin \alpha is another component of the force. If \displaystyle \mathbf{j} is vertical, \displaystyle F\sin \alpha is called the vertical component of the force.

If \displaystyle H is the horizontal component of the force and

\displaystyle V is the verical component of the force

The figure shows

\displaystyle {{F}^{2}}={{H}^{2}}+{{V}^{2}}

and also how to calculate the angles \displaystyle \alpha and \displaystyle \beta, for example,

\displaystyle \tan \alpha =\frac{V}{H} if \displaystyle H and \displaystyle V are known.

Note

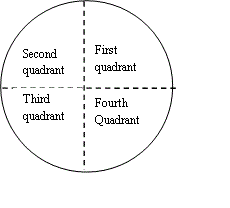
This equation has infinitely many solutions as if \displaystyle \alpha is a solution then \displaystyle \alpha \pm 180 is also a solution.

In this course it is assumed the solution chosen is between \displaystyle -180<\alpha \le 180. Then this equation always has two solutions for \displaystyle \alpha , giving two distinct directions. The solution in the quadrant that corresponds to the direction of the vector must be chosen.

Example 4.1

Express each of the forces given below in the form a\displaystyle \mathbf{i} + b\displaystyle \mathbf{j}.

a)

b)

Solution

a) \displaystyle 20\cos 40{}^\circ \mathbf{i}+20\sin 40{}^\circ \mathbf{j}\ \text{N}

b) \displaystyle -80\cos 30{}^\circ \mathbf{i}+80\sin 30{}^\circ \mathbf{j}\ \text{N}

Note the negative sign here in the first term.

Example 4.2

Express the force shown below as a vector in terms of \displaystyle \mathbf{i} and \displaystyle \mathbf{j}.

Solution

\displaystyle 28\cos 30{}^\circ \mathbf{i}-28\sin 30{}^\circ \mathbf{j}\ \text{N}

Note the negative sign in the second term.

Example 4.3

Express the force shown below as a vector in terms of \displaystyle \mathbf{i} and \displaystyle \mathbf{j}

Solution

\displaystyle -50\cos 44{}^\circ \mathbf{i}-50\sin 44{}^\circ \mathbf{j}\ \text{N}

Note that here both terms are negative.

Example 4.4

Find the magnitude of the force (4\displaystyle \mathbf{i} - 8\displaystyle \mathbf{j}) N. Draw a diagram to show the direction of this force.

Solution

The magnitude, \displaystyle F , of the force is given by,

\displaystyle F=\sqrt{{{4}^{2}}+{{8}^{2}}}=\sqrt{80}=8\textrm{.}94\text{ N (to 3sf)}

The angle, \displaystyle \theta , is given by,

\displaystyle \theta ={{\tan }^{-1}}\left( \frac{8}{4} \right)=63\textrm{.}4{}^\circ

Example 4.5

Find the magnitude and direction of the resultant of the four forces shown in the diagram.

Solution

Force	Vector Form (N)
20 N	\displaystyle 20\cos 50{}^\circ \mathbf{i}+20\sin 50{}^\circ \mathbf{j}
18 N	\displaystyle -18\mathbf{j}
25 N	\displaystyle -25\cos 20{}^\circ \mathbf{i}-25\sin 20{}^\circ \mathbf{j}
15 N	\displaystyle -15\cos 30{}^\circ \mathbf{i}+15\sin 30{}^\circ \mathbf{j}

\displaystyle \begin{align} & \text{Resultant Force }=\text{ }\left( 20\cos 50{}^\circ -25\cos 20{}^\circ -15\cos 30{}^\circ \right)\mathbf{i}+ \\ & \left( 20\sin 50{}^\circ -18-25\sin 20{}^\circ +15\sin 30{}^\circ \right)\mathbf{j}=-23.627\mathbf{i}-3.730\mathbf{j} \text{ N} \end{align}

The magnitude is given by:

\displaystyle \sqrt{{{23\textrm{.}627}^{2}}+{{3\textrm{.}730}^{2}}}=23\textrm{.}9\text{ N (to 3sf)}

The angle \displaystyle \theta can be found using tan.

\displaystyle \begin{align} & \tan \theta =\frac{3\textrm{.}730}{23\textrm{.}627} \\ & \theta =9\textrm{.}0{}^\circ \end{align}