Processing Math: Done

From Mechanics

Revision as of 11:41, 9 February 2010 (edit) Ian (Talk | contribs) ← Previous diff		Revision as of 15:32, 15 February 2010 (edit) (undo) Ian (Talk | contribs) Next diff →
Line 23:		Line 23:
	| valign="top"| <math>v</math> = final velocity		| valign="top"| <math>v</math> = final velocity
	|-		|-
-	| <math>{{v}^{2}}={{u}^{2}}+2as</math>	+	| <math>{{v}^{\ 2}}={{u}^{\ 2}}+2as</math>
	|valign="top"| <math>a</math> = acceleration		|valign="top"| <math>a</math> = acceleration
	|-		|-
-	| <math>s=ut+\frac{1}{2}a{{t}^{2}}</math>	+	| <math>s=ut+\frac{1}{2}a{{t}^{\ 2}}</math>
	|valign="top"|<math>s</math> = displacement		|valign="top"|<math>s</math> = displacement
Line 137:		Line 137:
	Using the equation		Using the equation
-	<math>{{v}^{2}}={{u}^{2}}+2as</math>	+	<math>{{v}^{\ 2}}={{u}^{\ 2}}+2as</math>
	gives:		gives:
Line 165:		Line 165:
	a) Using		a) Using
-	<math>s=ut+\frac{1}{2}a{{t}^{2}}</math>	+	<math>s=ut+\frac{1}{2}a{{t}^{\ 2}}</math>
	gives:		gives:
	<math>\begin{align}		<math>\begin{align}
-	& 10=0\times t+\frac{1}{2}\times 9\textrm{.}8{{t}^{2}} \\	+	& 10=0\times t+\frac{1}{2}\times 9\textrm{.}8{{t}^{\ 2}} \\
-	& 10=4\textrm{.}9{{t}^{2}} \\	+	& 10=4\textrm{.}9{{t}^{\ 2}} \\
	& t=\sqrt{\frac{10}{4\textrm{.}9}}=1\textrm{.}43\text{ s (to 3sf)} \\		& t=\sqrt{\frac{10}{4\textrm{.}9}}=1\textrm{.}43\text{ s (to 3sf)} \\
	\end{align}</math>		\end{align}</math>
	b) Using		b) Using
-	<math>{{v}^{2}}={{u}^{2}}+2as</math>	+	<math>{{v}^{\ 2}}={{u}^{\ 2}}+2as</math>
	gives:		gives:
	<math>\begin{align}		<math>\begin{align}
-	& {{v}^{2}}={{0}^{2}}+2\times 9\textrm{.}8\times 10 \\	+	& {{v}^{\ 2}}={{0}^{2}}+2\times 9\textrm{.}8\times 10 \\
	& v=\sqrt{196}=14\text{ m}{{\text{s}}^{\text{-1}}} \\		& v=\sqrt{196}=14\text{ m}{{\text{s}}^{\text{-1}}} \\
	\end{align}</math>		\end{align}</math>
Line 200:		Line 200:
	Using		Using
-	<math>{{v}^{2}}={{u}^{2}}+2as</math>	+	<math>{{v}^{\ 2}}={{u}^{\ 2}}+2as</math>
	gives;		gives;
Line 216:		Line 216:
	Using		Using
-	<math>s=ut+\frac{1}{2}a{{t}^{2}}</math>	+	<math>s=ut+\frac{1}{2}a{{t}^{\ 2}}</math>
	gives:		gives:
	<math>\begin{align}		<math>\begin{align}
-	& -2=9t+\frac{1}{2}\times (-10){{t}^{2}} \\	+	& -2=9t+\frac{1}{2}\times (-10){{t}^{\ 2}} \\
-	& -2=9t-5{{t}^{2}} \\	+	& -2=9t-5{{t}^{\ 2}} \\
-	& 5{{t}^{2}}-9t-2=0 \\	+	& 5{{t}^{\ 2}}-9t-2=0 \\
	& (5t+1)(t-2)=0 \\		& (5t+1)(t-2)=0 \\
	& t=-\frac{1}{5}\text{ or }t=2 \\		& t=-\frac{1}{5}\text{ or }t=2 \\
Line 247:		Line 247:
	a) Using		a) Using
-	<math>{{v}^{2}}={{u}^{2}}+2as</math>	+	<math>{{v}^{\ 2}}={{u}^{\ 2}}+2as</math>
	we can find the distance travelled:		we can find the distance travelled:

---

Revision as of 15:32, 15 February 2010

Theory

Exercises

Key Points

Constant Acceleration Equations

v=u+at	u = initial velocity
s=21(u+v)t	v = final velocity
v 2=u 2+2as	a = acceleration
s=ut+21at 2	s = displacement
	t = time

Only use the constant acceleration formulae when the acceleration is constant or can be assumed to be constant.

Interpreting Graphs

The gradient of a "displacement – time" graph gives the velocity.

The gradient of a "velocity - time" graph gives the acceleration.

The area under a "velocity – time" graph can be used to find the displacement.

Link with Calculus

v=dtds and a=dtdv

Example 6.1

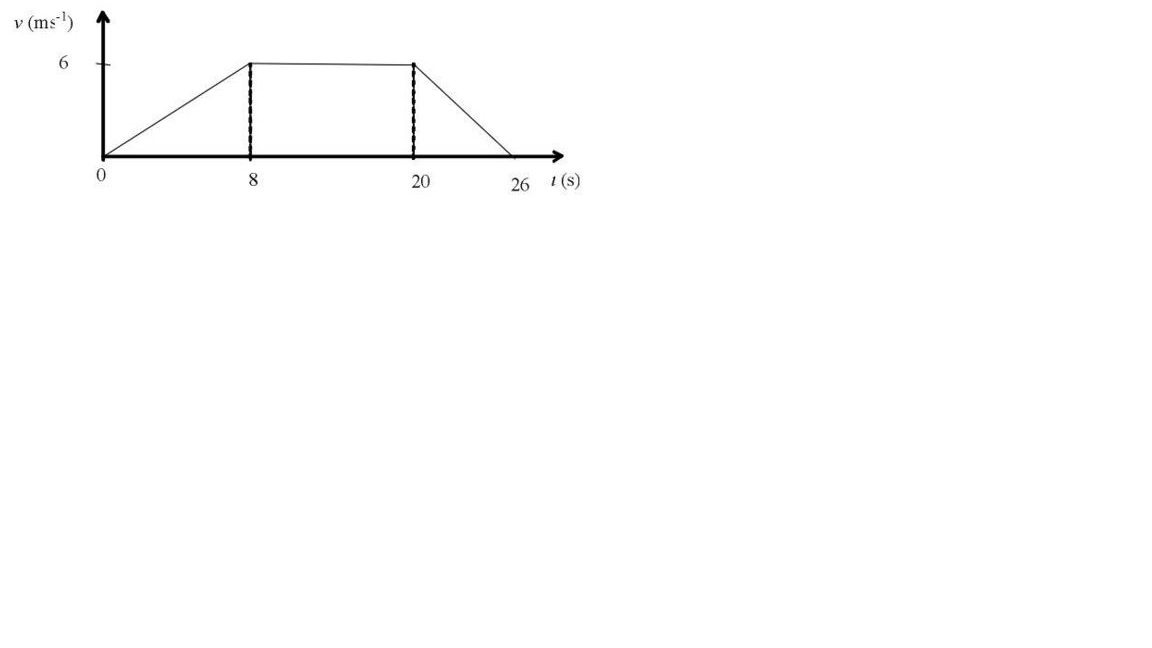
The graph shows how the velocity of a car changes as it moves a short distance along a straight road.

a) Find the total distance travelled by the car.

b) Calculate the acceleration of the car on each on each stage of its journey.

Solution

(a) The total distance travelled by the car is given by the area under the graph.

Using the formula for the area of a trapezium gives:

s=21(12+26)6=114 m

Alternatively, breaking the area under the graph into three parts gives.

s=2186+126+2166=24+72+18=114 m 

(b) The acceleration of the car on each stage of the journey is given by the gradient of the graph.

Stage 1: a=86=0.75 ms-2

Stage 2: a=0 (Since the graph is horizontal.)

Stage 3: a=−66=−1 ms-2

Example 6.2

As a car travels along a straight road its speed increases from 10 ms−1 to 35 ms−1 in 50 seconds.

a) Calculate the distance travelled by the car.

b) Find the acceleration of the car.

c) Find the distance travelled when the speed of the car is 20 ms−1.

Solution

To start with we have u=10 , v=35 and t=50 .

a) Using s=21(u+v)t gives:

s=21(10+35)50=1125 m

b) Using v=u+at gives:

35=10+50a25=50aa=5025=0.5 ms-2

c) We now have to work with u=10 , v=20 and a=0.5 .

Using the equation v 2=u 2+2as gives:

202=102+20.5s400=100+ss=300 m

Example 6.3

A ball is dropped from a height of 10 m and falls until it hits the ground. Assume that no resistance forces act on the ball as it falls.

a) Find the time that it takes the ball to reach the ground.

b) Find the speed of the ball when it hits the ground.

Solution

In this case we have u=0 , a=9.8 and s=10

a) Using s=ut+21at 2 gives:

10=0t+219.8t 210=4.9t 2t=104.9=1.43 s (to 3sf)

b) Using v 2=u 2+2as gives:

v 2=02+29.810v=196=14 ms-1

Example 6.4

A ball is thrown vertically upwards at a speed of 9 ms−1, from a height of 2 m. Find the maximum height of the ball and the time it is in the air. Assume g = 10 ms−2.

Solution

In this case u=9 and a=−10 At its maximum height we also have v=0 .

Using v 2=u 2+2as gives;

02=92+2(−10)s0=81−20ss=2081=4.05 m

But as the ball is thrown from a height of 2m, it reaches a maximum of 6.05 metres above ground level.

As the ball lands 2 metres below its initial position, we have s=−2 when it hits the ground.

Using s=ut+21at 2 gives:

−2=9t+21(−10)t 2−2=9t−5t 25t 2−9t−2=0(5t+1)(t−2)=0t=−51 or t=2

We need a positive time and the ball must be in the air for 2 seconds.

Example 6.5

A lorry is initially travelling at 18 ms−1, when the driver applies the brakes. Assume that the acceleration of the lorry remains constant at -1.2 ms−2 until it stops. (a) Find the distance that the lorry travels before stopping. (b) Find the time that it takes for the lorry to stop.

Solution

In this case we have u=18 , a=−1.2 and since the lorry comes to rest v=0 .

a) Using v 2=u 2+2as we can find the distance travelled:

02=182+2(−1.2)s324−24s=0s=2.4324=135 m

Using v=u+at we can find the time taken:

0=10+(−0.8)t0=10−0.8tt=100.8=12.5 s