Practice Test Paper 2
From Mechanics
| Line 2: | Line 2: | ||
| - | '''Note that the Mechanics Test | + | '''Note that the Mechanics Test accounts for <math> \bf 50\%</math> of the final mechanics mark.''' |
Current revision
\displaystyle \large {\underline{ {\textbf {Practice Test Paper (1 hour)}}}}
Note that the Mechanics Test accounts for \displaystyle \bf 50\% of the final mechanics mark.
1. A ball is released from rest at a height of 44.1 metres. Assume that the ball is a particle and that no resistance forces act on it as it moves.
(a) Show that it takes 3 seconds for the ball to fall the 44.1 metres.
(3 marks)
(b) Find the speed of the ball when it has fallen the 44.1 metres.
(3 marks)
(c) Explain why your answer to part (b) would be less in reality.
(1 mark)
2. A car and its passengers have a total mass of 2000 kg. The car travels along a straight horizontal road. As it moves it experiences a forward driving force of magnitude \displaystyle P newtons and a constant resistance force of 900 newtons. Assume that the car is modelled as a particle.
(a) Draw a diagram to show the horizontal forces acting on the car.
(1 mark)
(b) State the value of \displaystyle P if the car travels at a constant speed.
(1 mark)
(c) Find the value of \displaystyle P if the car accelerates at 1.2 \displaystyle \text{ m}{{\text{s}}^{-2} }.
(3 marks)
(d) If \displaystyle P = 800, find the acceleration of the car and describe what is happening to the speed of the car.
(4 marks)
3. A block of mass 20 kg is placed on a rough horizontal surface. The coefficient of friction between the block and the surface is 0.4.
(a) Calculate the magnitude of the normal reaction force on the block.
(2 marks)
(b) Calculate the maximum magnitude of the friction force.
(2 marks)
(c) A horizontal force of 100 N acts on the block. Find the acceleration of the block.
(3 marks)
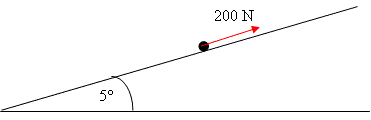
4. A crate, of mass 100 kg, is pulled up a slope by a force of 200 N, which acts parallel to the slope, as shown in the diagram. The slope is inclined at \displaystyle 5{}^\circ to the horizontal. Model the crate as a particle
Assume that the slope is smooth.
(a) Draw a diagram to show the forces acting on the crate if the slope is smooth.
(1 mark)
(b) Show that the acceleration of the crate is 1.15 \displaystyle \text{ m}{{\text{s}}^{-2} }, correct to three significant figures.
(4 marks)
(c) Find the distance that the crate would travel up the slope in 5 seconds if it starts at rest.
(3 marks)
5. A particle is initially at the origin, O, and has velocity \displaystyle (6\mathbf{i}+4\mathbf{j})\text{ m}{{\text{s}}^{\text{-1}}}. It moves with constant acceleration of \displaystyle (0\textrm{.}2\mathbf{i}-0\textrm{.}4\mathbf{j})\text{ m}{{\text{s}}^{\text{-2}}} . The unit vectors \displaystyle \mathbf{i} and \displaystyle \mathbf{j} are directed east and north respectively.
(a) Find an expression for the velocity of the particle at time \displaystyle t seconds.
(2 marks)
(b) At the point A, the particle is moving due east. Find the time that it takes for the particle to move from O to A.
(3 marks)
(c) The particle reaches the point B, 30 seconds after it has left the origin. Find the distance between the origin, O, and the point B.
(4 marks)
40 MARKS