Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution to Test Paper 2

From Mechanics

(Difference between revisions)
Jump to: navigation, search
Line 6: Line 6:
| 1 (a)
| 1 (a)
| <math>\begin{align}
| <math>\begin{align}
-
& 44 \ \textrm{.}1=\frac{1}{2}\times 9 \textrm{.} 8{{t}^{2}} \\
+
& 44\textrm{.}1=\frac{1}{2}\times 9\textrm{.}8{{t}^{2}} \\
-
& t=\sqrt{\frac{44 \textrm{.}1}{4 \textrm{.}9}}=3\text{ s} \\
+
& t=\sqrt{\frac{44\textrm{.}1}{4\textrm{.}9}}=3\text{ s} \\
-
\end{align}</math>
+
& \\
-
 
+
& \text{OR} \\
-
OR
+
& \\
-
 
+
& s=\frac{1}{2}\times 9\textrm{.}8\times {{3}^{2}}=44\textrm{.}1 \\
-
<math>\begin{align}
+
-
& s=\frac{1}{2}\times 9 \textrm{.}8\times {{3}^{2}}=44 \textrm{.}1 \\
+
-
& \text{AG} \\
+
& \therefore \text{Hits ground after 3 seconds} \\
& \therefore \text{Hits ground after 3 seconds} \\
\end{align}</math>
\end{align}</math>
-
 
+
AG
Line 49: Line 46:
| 1 (b)
| 1 (b)
| <math>\begin{align}
| <math>\begin{align}
-
& {{v}^{2}}={{0}^{2}}+2\times 9 \textrm{.}8\times 44 \textrm{.}1 \\
+
& {{v}^{2}}={{0}^{2}}+2\times 9\textrm{.}8\times 44\textrm{.}1 \\
-
& v=\sqrt{864 \textrm{.}36}=29 \ \textrm{.}4\text{ m}{{\text{s}}^{-1}} \\
+
& v=\sqrt{864\textrm{.}36}=29\textrm{.}4m \\
 +
& \\
 +
& \text{OR} \\
 +
& \\
 +
& v=0+9\textrm{.}8\times 3 \\
 +
& v=29\textrm{.}4 \\
\end{align}</math>
\end{align}</math>
-
OR
 
- 
-
<math>\begin{align}
 
-
& v=0+9 \textrm{.}8\times 3 \\
 
-
& v=29 \textrm{.}4 \text{ m}{{\text{s}}^{-1}} \\
 
-
\end{align}</math>
 

Revision as of 10:06, 8 April 2012

Solutions
1 (a) 44.1=219.8t2t=4.944.1=3 sORs=219.832=44.1Hits ground after 3 secondsAGM1

A1

A1


(M1)

(A1)

(A1)


(3 marks) M1: Use of constant acceleration

equation with v=0

A1: Correct equation

A1: Correct s


1 (b) v2=02+29.844.1v=864.36=29.4mORv=0+9.83v=29.4M1

A1

A1


(3 marks)


M1: Use of constant acceleration equation with v=0

A1: Correct equation.

A1: Correct v.


1 (c) Air resistance would slow the ball down. B1 (1 mark) B1: Sensible statement about air resistance.
(7 marks)
2 (a) Image:test2ans2.gif B1 (1 mark) B1: Correct horizontal forces.

Ignore any vertical forces.


2 (b) P=900N B1 (1 mark) B1: Correct value for P.
2 (c) P−900=20001.2P=2400+900=3300N M1

A1

A1

(1 mark) M1: Three term equation of motion

A1: Correct equation

A1: Correct P.


2 (d) 800−900=2000aa=2000−100=−0.05 ms−2Carisslowingdown M1

A1

A1

A1

(4 marks) M1: Three term equation of motion

A1: Correct equation

A1: Correct a

A1: Correct statement


(9 marks)
3 (a) R=209.8=196 N M1

A1

(2 marks) M1: Use of R=mg

A1: Correct R.


3 (b) F=0.4196=78.4 N M1

A1

(2 Marks) M1: Use of F=R

A1: Correct F.


3 (c) 100−78.4=20aa=20100−78.4=1.08 ms−2 M1

A1

A1

(3 marks) M1: Three term equation of motion

A1: Correct equation

A1: Correct a.


(8 marks)
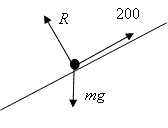
4 (a) Image:test2ans4.gif B1 (1 mark) B1: Correct force diagram
4 (b) 100a=200−980sin5a=100200−980sin5=1.15 ms−2 M1A1

M1

A1

(4 marks) M1: Three term equation of motion

A1: Correct equation

M1: Rearranging equation.

A1: Correct a.


4 (c)

s=05+211.1552=14.4 m

M1

A1

A1

(3 marks) M1: Using a constant acceleration equation

A1: Correct equation

A1: Correct distance.


(8 marks)
5 (a) v=(6i+4j)+(0.2i−0.4j)t M1

A1

(2 marks) M1: Use of v=u+at

A1: Correct expression


5 (b) 4−0.4t=0t=10 s M1

A1

A1

(3 marks) M1: Using j component equal to zero.

A1: Correct equation.

A1: Correct time.

5 (c) r=(6i+4j)30+21(0.2i−0.4j)302=270i−60jr=2702+602=277 m M1

A1

M1

A1

(4 marks) M1: Using r=ut+21at2

A1: Correct position vector.

M1: Finding distance.

A1: Correct distance

(8 marks)


KEY M1: Method Mark

A1: Accuracy Mark following a method mark

B1: Accuracy Mark not following a method mark

AG: Answer Given in Question – Working must justify answer.

TOTAL: 40 Marks

Retrieved from "http://wiki.math.se/wikis/2009/bridgecoursemechanics/index.php/Solution_to_Test_Paper_2"