Processing Math: Done

From Mechanics

Theory

Exercises

5. Forces and Equilibrium

Key Points

If the resultant of the forces acting on a particle is zero we say that these forces are in equilibrium.

Example 5.1

The diagram shows an object, of mass 300 kg, that is at rest and is supported by two cables. Find the tension in each cable.

Solution

The diagram shows the forces acting on the object.

Resolving horizontally or using the horizontal components of the forces:

T1cos60=T2cos60T1=T2

Resolving vertically gives;

T1sin60+T2sin60=2940

Now solving the equations by substituting T1=T2 gives:

T1sin60+T2sin60=29402T1sin60=2940T1=29402sin60=1700 N (to 3sf)

And also T2=1700 N (to 3 sf) .

Example 5.2

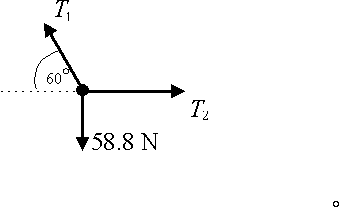
A particle of mass 6 kg is suspended by two strings as shown in the diagram. Note that one string is horizontal. Find the tension in each string.

Solution

The diagram shows the forces acting on the particle.

Resolving vertically:

T1sin60=588T1=588sin60=679 N (to 3 sf)

Resolving horizontally:

T1cos60=T2T2=588sin60cos60=339 N (to 3sf)

Example 5.3

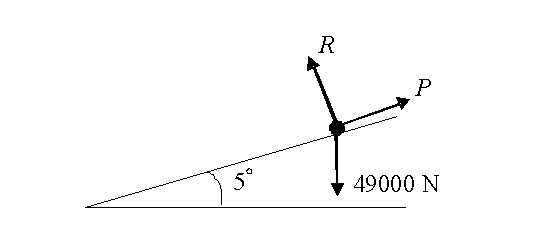
A lorry of mass 5000 kg drives up a slope inclined at 5 to the horizontal. The lorry moves in a straight line and at a constant speed. Assume that no resistance forces act on the lorry. Find the magnitude of the normal reaction force and force that acts on the lorry in its direction of motion.

Solution

Model the lorry as a particle.

The diagram shows the forces acting on the lorry.

Resolving perpendicular to the slope gives:

R=49000cos5=48800 N (to 3 sf)

Resolving parallel to the slope gives:

P=49000sin5=4270 N (to 3sf)

Example 5.4

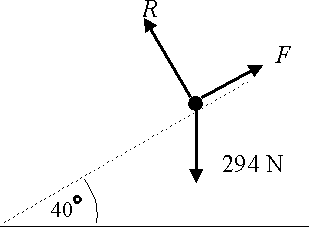
A child, of mass 30kg, slides down a slide at a constant speed. Assume that there is no air resistance acting on the child. The slide makes an angle of 40 with the horizontal. Find the magnitude of the friction force on the child and the coefficient of friction.

Solution

Model the child as a particle.

The diagram shows the forces acting on the child.

Resolving parallel to the slope gives.

F=294sin40=189 N (to 3sf)

Resolving perpendicular to the slope gives:

R=294cos40

As the child is sliding F=R so that we can determine .

294sin40=294cos40=294sin40294cos40=tan40=0840 (to 3 sf)

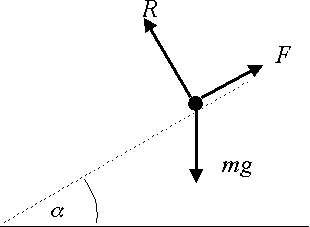
Note – Angle of Friction

If a particle of mass m is at rest on a slope at an angle  above the horizontal, then :

F=mgsin

R=mgcos

Then using FR gives:

mgsinmgcossincostan

Example 5.5

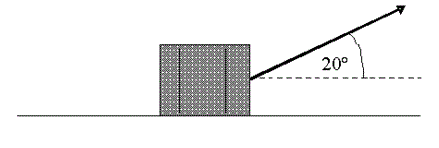
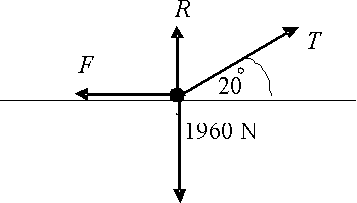
A crate of mass 200 kg is on a horizontal surface. The coefficient of friction between the crate and the surface is 0.4. The crate is pulled by a rope, as shown in the diagram, so that the crate moves at a constant speed in a straight line. Find the tension in the rope.

Solution

The diagram shows the forces acting on the crate.

Resolving horizontally:

F=Tcos20

Resolving vertically:

R+Tsin20=1960

or

R=1960−Tsin20

As the crate is sliding we can use F=R, which gives:

F=04R

Using this equation with the horizontal and vertical equations gives:

Tcos20=041960−Tsin20Tcos20=784−T04sin20Tcos20+T04sin20=784Tcos20+04sin20=784T=784cos20+04sin20=728 N (to 3sf)