Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Solution to Test Paper 1

From Mechanics

Revision as of 17:58, 18 January 2011 by Ian (Talk | contribs)
Jump to: navigation, search
Solutions
1 (a) 02=72+2(−.8)ss=4919.6=2.5Max Height = 5+2.5=7.5 m (3 marks)


1 (b) 0=7−9.8tt=79.8=0.714 s (3 marks)
(6 marks)


2 (a) T−8009.8=8000.2T=7840+160=8000 N (3 marks)


2 (b) T−8009.8=800(−0.2)T=7840−160=7680 N (3 marks)


2 (c) T=8009.8=7840 N (1 mark)


(7 marks)


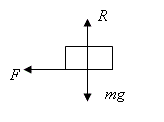
3 (a) Image:test1ans1.gif (1 mark)


3 (b) F=21.8=3.6 N (2 marks)


3 (c) R=29.8=19.6 N (2 marks)


3 (d) 3.6=19.6=3.619.6=0.184 (3 marks)


(8 marks)


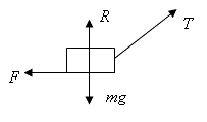
4 (a) Image:test1ans2.gif (1 mark)


4 (b) R+Tsin30=2009.8R+0.5T=1960R=1960−0.5T (3 marks)


4 (c)

F=Tcos30Tcos30=0.6(1960−0.5T)T(cos30+0.3)=1176T=1176(cos30+0.3)=1010 N

(4 marks)


(8 marks)


5 (a) 5i−2j=4i+3j+10aa=110(i−5j)=0.1i−0.5j ms-2  (3 marks)


5 (b) r=(4i+3j)t+0.5(0.1i−0.5j)t2 (2 marks)


5 (c) r=(4t+0.05t2)i+(3t−0.25t2)j3t−0.25t2=0t(3−0.25t)=0t=0 or t=30.25=12 st=12 s (3 marks)


5 (d) v=(4+0.1t)i+(3−0.5t)j3−0.5t=0t=6 s (3 marks)


(11 marks)


Retrieved from "http://wiki.math.se/wikis/2009/bridgecoursemechanics/index.php/Solution_to_Test_Paper_1"