2.2 Övningar
FörberedandeFysik
| (11 mellanliggande versioner visas inte.) | |||
| Rad 12: | Rad 12: | ||
[[Bild:vektor1.jpg]]<br\> | [[Bild:vektor1.jpg]]<br\> | ||
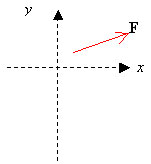
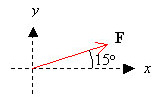
| - | Beloppet av kraften | + | Beloppet av kraften <math>\mathbf F</math> är <math>F=500 \,\mathrm N</math>. Skriv <math>\mathbf F</math> som vektor. |
</div>{{#NAVCONTENT:Svar|Svar 2.2:1|Lösning |Lösning 2.2:1}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:1|Lösning |Lösning 2.2:1}} | ||
| Rad 18: | Rad 18: | ||
===Övning 2.2:2=== | ===Övning 2.2:2=== | ||
<div class="ovning"> | <div class="ovning"> | ||
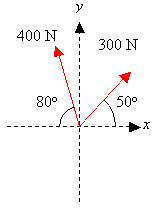
| - | Vilken är resultanten | + | Vilken är resultanten <math>\mathbf R</math> till de två krafterna i figuren?<br\> |
[[Bild:vektor2.jpg]] | [[Bild:vektor2.jpg]] | ||
| Rad 28: | Rad 28: | ||
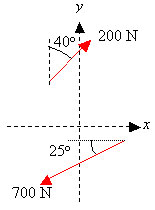
[[Bild:vektor3.jpg]]<br\> | [[Bild:vektor3.jpg]]<br\> | ||
| - | Vilken är resultanten | + | Vilken är resultanten <math>\mathbf R</math> till de två krafterna i figuren? |
</div>{{#NAVCONTENT:Svar|Svar 2.2:3|Lösning |Lösning 2.2:3}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:3|Lösning |Lösning 2.2:3}} | ||
| Rad 34: | Rad 34: | ||
===Övning 2.2:4=== | ===Övning 2.2:4=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| - | Krafterna | + | Krafterna <math>\mathbf F=(8,12)\,\mathrm N</math> och <math>\mathbf G=(-12,8) \,\mathrm N</math> är givna. Beräkna resultanten. <math>\mathbf R=3\mathbf F+4\mathbf G</math> |
</div>{{#NAVCONTENT:Svar|Svar 2.2:4|Lösning |Lösning 2.2:4}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:4|Lösning |Lösning 2.2:4}} | ||
| Rad 40: | Rad 40: | ||
===Övning 2.2:5=== | ===Övning 2.2:5=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | [[Bild:vektor5.jpg]]<br\> | ||
| + | I figuren är vektorn <math>\mathbf F=(45,3; 19,4) \,\mathrm N</math> utritad. Ange och rita ut vektorn <math>-\mathbf F/2</math>. | ||
</div>{{#NAVCONTENT:Svar|Svar 2.2:5|Lösning |Lösning 2.2:5}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:5|Lösning |Lösning 2.2:5}} | ||
| Rad 46: | Rad 48: | ||
===Övning 2.2:6=== | ===Övning 2.2:6=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | Bestäm två enhetsvektorer <math>\mathbf e_F</math> som är parallella med <math>\mathbf F=(6,10) \,\mathrm N</math>. | ||
</div>{{#NAVCONTENT:Svar|Svar 2.2:6|Lösning |Lösning 2.2:6}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:6|Lösning |Lösning 2.2:6}} | ||
| Rad 52: | Rad 55: | ||
===Övning 2.2:7=== | ===Övning 2.2:7=== | ||
<div class="ovning"> | <div class="ovning"> | ||
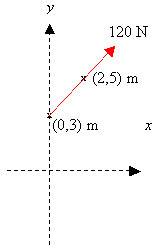
| + | [[Bild:vektor7.jpg]]<br\> | ||
| + | |||
| + | En kraft vars belopp är <math>120 \,\mathrm N</math> angriper i punkten <math>(0, 3) \,\mathrm{dm}</math> och dess verkningslinje går genom punkten <math>(2, 5)\,\mathrm{dm}</math> i <math>xy</math>-planet. Skriv kraften som vektor. | ||
</div>{{#NAVCONTENT:Svar|Svar 2.2:7|Lösning |Lösning 2.2:7}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:7|Lösning |Lösning 2.2:7}} | ||
| Rad 58: | Rad 64: | ||
===Övning 2.2:8=== | ===Övning 2.2:8=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| - | + | Vektorerna <math>\mathbf b = (3, -1)</math>, <math>\mathbf c = (-2, 4)</math> och <math>\mathbf d = (1, 2)</math> är givna. Bestäm en enhetsvektor parallell med <math>2 \mathbf b - \mathbf c + 3 \mathbf d</math> | |
| + | . | ||
</div>{{#NAVCONTENT:Svar|Svar 2.2:8|Lösning |Lösning 2.2:8}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:8|Lösning |Lösning 2.2:8}} | ||
| Rad 64: | Rad 71: | ||
===Övning 2.2:9=== | ===Övning 2.2:9=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | En skidåkare åker först <math>3,2</math> km åt nordväst och sedan <math>2,3</math> km rakt söderut. | ||
| + | Beskriv hans förflyttning som vektor om <math>x</math>-axeln pekar rakt österut och <math>y</math>-axeln pekar rakt norrut. | ||
</div>{{#NAVCONTENT:Svar|Svar 2.2:9|Lösning |Lösning 2.2:9}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:9|Lösning |Lösning 2.2:9}} | ||
| Rad 70: | Rad 79: | ||
===Övning 2.2:10=== | ===Övning 2.2:10=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| - | + | Vektorerna <math>\mathbf b = (3, -1)</math>, <math>\mathbf c = (-2, 4)</math> är givna. Bestäm en vektor <math>\mathbf d</math> så att <math>\mathbf b + \mathbf c + \mathbf d = \mathbf 0</math>, dvs nollvektorn. | |
</div>{{#NAVCONTENT:Svar|Svar 2.2:10|Lösning |Lösning 2.2:10}} | </div>{{#NAVCONTENT:Svar|Svar 2.2:10|Lösning |Lösning 2.2:10}} | ||
Nuvarande version
| Teori | Övningar |
Övning 2.2:1
Beloppet av kraften \displaystyle \mathbf F är \displaystyle F=500 \,\mathrm N. Skriv \displaystyle \mathbf F som vektor.
Hämtar...
Övning 2.2:2
Vilken är resultanten \displaystyle \mathbf R till de två krafterna i figuren?
Övning 2.2:3
Vilken är resultanten \displaystyle \mathbf R till de två krafterna i figuren?
Övning 2.2:4
Krafterna \displaystyle \mathbf F=(8,12)\,\mathrm N och \displaystyle \mathbf G=(-12,8) \,\mathrm N är givna. Beräkna resultanten. \displaystyle \mathbf R=3\mathbf F+4\mathbf G
Övning 2.2:5
I figuren är vektorn \displaystyle \mathbf F=(45,3; 19,4) \,\mathrm N utritad. Ange och rita ut vektorn \displaystyle -\mathbf F/2.
Övning 2.2:6
Bestäm två enhetsvektorer \displaystyle \mathbf e_F som är parallella med \displaystyle \mathbf F=(6,10) \,\mathrm N.
Övning 2.2:7
En kraft vars belopp är \displaystyle 120 \,\mathrm N angriper i punkten \displaystyle (0, 3) \,\mathrm{dm} och dess verkningslinje går genom punkten \displaystyle (2, 5)\,\mathrm{dm} i \displaystyle xy-planet. Skriv kraften som vektor.
Övning 2.2:8
Vektorerna \displaystyle \mathbf b = (3, -1), \displaystyle \mathbf c = (-2, 4) och \displaystyle \mathbf d = (1, 2) är givna. Bestäm en enhetsvektor parallell med \displaystyle 2 \mathbf b - \mathbf c + 3 \mathbf d .
Övning 2.2:9
En skidåkare åker först \displaystyle 3,2 km åt nordväst och sedan \displaystyle 2,3 km rakt söderut. Beskriv hans förflyttning som vektor om \displaystyle x-axeln pekar rakt österut och \displaystyle y-axeln pekar rakt norrut.
Övning 2.2:10
Vektorerna \displaystyle \mathbf b = (3, -1), \displaystyle \mathbf c = (-2, 4) är givna. Bestäm en vektor \displaystyle \mathbf d så att \displaystyle \mathbf b + \mathbf c + \mathbf d = \mathbf 0, dvs nollvektorn.
