2.2 Övningar

Beloppet av kraften F är F\displaystyle =500N. Skriv F som vektor.

Vilken är resultanten R till de två krafterna i figuren?

Vilken är resultanten R till de två krafterna i figuren?

Krafterna F\displaystyle =(8,12)N och G\displaystyle =(-12,8)N är givna. Beräkna resultanten. R\displaystyle =3F\displaystyle +4G

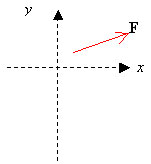
I figuren är vektorn F\displaystyle =(45,3; 19,4)N utritad. Ange och rita ut vektorn -F\displaystyle /2.

Bestäm två enhetsvektorer \displaystyle e_F som är parallella med F\displaystyle =(6,10)N.

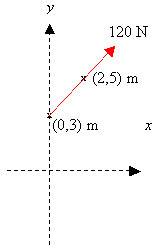
En kraft vars belopp är \displaystyle 120 N angriper i punkten \displaystyle (0, 3) dm och dess verkningslinje går genom punkten \displaystyle (2, 5) dm i xy-planet. Skriv kraften som vektor.

Vektorerna b\displaystyle = (3, -1), c\displaystyle = (-2, 4) och d\displaystyle = (1, 2) är givna. Bestäm en enhetsvektor parallell med \displaystyle 2b\displaystyle – c\displaystyle + 3d.

En skidåkare åker först \displaystyle 3,2 km åt nordväst och sedan \displaystyle 2,3 km rakt söderut. Beskriv hans förflyttning som vektor om \displaystyle x-axeln pekar rakt österut och \displaystyle y-axeln pekar rakt norrut.

Vektorerna b\displaystyle = (3, -1), c\displaystyle = (-2, 4) är givna. Bestäm en vektor d så att b + c + d = 0, dvs nollvektorn.