Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 1.3:1b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 1.3:1b moved to Solution 1.3:1b: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
There are two points,
-
<center> [[Image:1_3_1b-1(3).gif]] </center>
+
<math>x=a</math>
-
{{NAVCONTENT_STOP}}
+
and
-
{{NAVCONTENT_START}}
+
<math>x=b</math>
-
<center> [[Image:1_3_1b-2(3).gif]] </center>
+
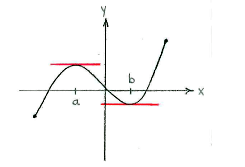
(see picture below), where the function has a horizontal tangent and hence a derivative equal to zero. These are the functions critical points.
-
{{NAVCONTENT_STOP}}
+
 
-
{{NAVCONTENT_START}}
+
-
<center> [[Image:1_3_1b-3(3).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
[[Image:1_3_1_b1.gif|center]]
[[Image:1_3_1_b1.gif|center]]
 +
 +
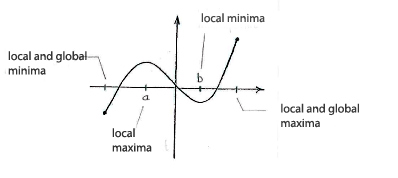
Furthermore, we see that the function has local minimum points at the left endpoint of the interval of definition and
 +
<math>x=b</math>, because the function takes higher values at neighbouring points. In the same way, we see that the function has local maximum points at
 +
<math>x=a</math>
 +
and at the right endpoint of the interval of definition.
 +
 +
Of these local extreme points, the left endpoint is a global minimum (that point where the function takes its absolute minimum value) and the right endpoint is a global maximum.
 +
 +
 +
 +
[[Image:1_3_1_b2.gif|center]]
[[Image:1_3_1_b2.gif|center]]
 +
 +
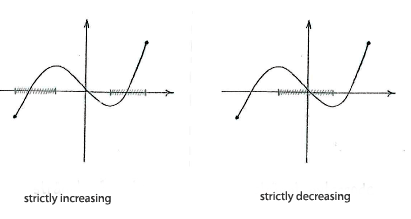
The function is strictly increasing (it has a tangent that slopes upwards) in the interval between the left endpoint and
 +
<math>x=a</math>, as well as between
 +
<math>x=b</math>
 +
and the right endpoint. In the interval between
 +
<math>x=0</math>
 +
and
 +
<math>x=b</math>, the function is strictly decreasing.
 +
 +
[[Image:1_3_1_b3.gif|center]]
[[Image:1_3_1_b3.gif|center]]

Version vom 09:11, 15. Okt. 2008

There are two points, x=a and x=b (see picture below), where the function has a horizontal tangent and hence a derivative equal to zero. These are the functions critical points.


Furthermore, we see that the function has local minimum points at the left endpoint of the interval of definition and x=b, because the function takes higher values at neighbouring points. In the same way, we see that the function has local maximum points at x=a and at the right endpoint of the interval of definition.

Of these local extreme points, the left endpoint is a global minimum (that point where the function takes its absolute minimum value) and the right endpoint is a global maximum.



The function is strictly increasing (it has a tangent that slopes upwards) in the interval between the left endpoint and x=a, as well as between x=b and the right endpoint. In the interval between x=0 and x=b, the function is strictly decreasing.


Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:1b“