Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 1.3:1a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
A critical point is a point where the derivative is equal to zero, i.e. the function has a horizontal tangent. For the function in the exercise, this occurs when
A critical point is a point where the derivative is equal to zero, i.e. the function has a horizontal tangent. For the function in the exercise, this occurs when
-
<math>\text{x}=0</math>.
+
<math>x=0</math>.
Zeile 8: Zeile 8:
In addition, the point at the origin is a local and global minimum, because no other points give a smaller value for the function that the point at
In addition, the point at the origin is a local and global minimum, because no other points give a smaller value for the function that the point at
-
<math>\text{x}=0</math>. On the other hand, there are no inflexion points (points where the derivative is both zero and has the same sign on both sides of the point).
+
<math>x=0</math>. On the other hand, there are no inflexion points (points where the derivative is both zero and has the same sign on both sides of the point).
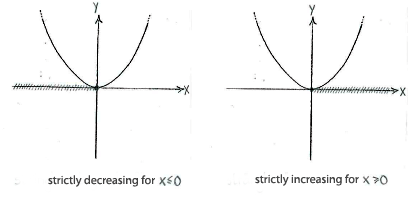
To the left of
To the left of
-
<math>\text{x}=0</math>, the derivative is negative (the tangent slopes downwards) and the function is strictly decreasing, and to the right of
+
<math>x=0</math>, the derivative is negative (the tangent slopes downwards) and the function is strictly decreasing, and to the right of
-
<math>\text{x}=0</math>
+
<math>x=0</math>
the derivative ) the tangent slopes upwards) and the function is strictly increasing.
the derivative ) the tangent slopes upwards) and the function is strictly increasing.
[[Image:1_3_1_a3.gif|center]]
[[Image:1_3_1_a3.gif|center]]

Version vom 09:14, 15. Okt. 2008

A critical point is a point where the derivative is equal to zero, i.e. the function has a horizontal tangent. For the function in the exercise, this occurs when x=0.



In addition, the point at the origin is a local and global minimum, because no other points give a smaller value for the function that the point at x=0. On the other hand, there are no inflexion points (points where the derivative is both zero and has the same sign on both sides of the point).

To the left of x=0, the derivative is negative (the tangent slopes downwards) and the function is strictly decreasing, and to the right of x=0 the derivative ) the tangent slopes upwards) and the function is strictly increasing.

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:1a“