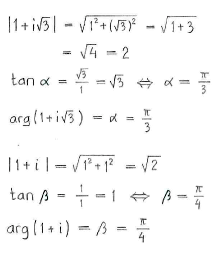Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 3.3:1d

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 3.3:1d moved to Solution 3.3:1d: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Because we are going to raise something to the power
-
<center> [[Image:3_3_1d-1(2).gif]] </center>
+
<math>\text{12}</math>, the base in the expression should be written in polar form. In turn, the base consists of a quotient which it is advantageous to calculate in polar form. Thus, it seems appropriate to write
-
{{NAVCONTENT_STOP}}
+
<math>1+i\sqrt{3}</math>
-
{{NAVCONTENT_START}}
+
and
-
<center> [[Image:3_3_1d-2(2).gif]] </center>
+
<math>\text{1}+i</math> in polar form right from the beginning and to carry out all calculations in polar form.
-
{{NAVCONTENT_STOP}}
+
 
[[Image:3_3_1_d.gif]] [[Image:3_3_1_d_text.gif]]
[[Image:3_3_1_d.gif]] [[Image:3_3_1_d_text.gif]]
 +
 +
 +
We obtain
 +
 +
 +
<math>\begin{align}
 +
& 1+i\sqrt{3}=2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right) \\
 +
& \text{1}+i=\sqrt{2}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right) \\
 +
\end{align}</math>
 +
 +
 +
and
 +
 +
 +
<math>\begin{align}
 +
& \frac{1+i\sqrt{3}}{\text{1}+i}=\frac{2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)}{\sqrt{2}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right)} \\
 +
& =\frac{2}{\sqrt{2}}\left( \cos \left( \frac{\pi }{3}-\frac{\pi }{4} \right)+i\sin \left( \frac{\pi }{3}-\frac{\pi }{4} \right) \right) \\
 +
& =\sqrt{2}\left( \cos \frac{\pi }{12}+i\sin \frac{\pi }{12} \right) \\
 +
& \\
 +
& \\
 +
& \\
 +
\end{align}</math>
 +
 +
 +
Finally, de Moivre's formula gives
 +
 +
 +
<math>\begin{align}
 +
& \left( \frac{1+i\sqrt{3}}{\text{1}+i} \right)^{12}=\left( \sqrt{2} \right)^{12}\left( \cos 12\centerdot \frac{\pi }{12}+i\sin 12\centerdot \frac{\pi }{12} \right) \\
 +
& =2^{\frac{1}{2}\centerdot 12}\left( \cos \pi +i\sin \pi \right) \\
 +
& =2^{6}\centerdot \left( -1+i\centerdot 0 \right) \\
 +
& =-64 \\
 +
\end{align}</math>

Version vom 07:49, 24. Okt. 2008

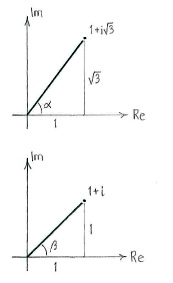
Because we are going to raise something to the power 12, the base in the expression should be written in polar form. In turn, the base consists of a quotient which it is advantageous to calculate in polar form. Thus, it seems appropriate to write 1+i3  and 1+i in polar form right from the beginning and to carry out all calculations in polar form.


Image:3_3_1_d.gif Image:3_3_1_d_text.gif


We obtain


1+i3=2cos3+isin31+i=2cos4+isin4 


and


1+i1+i3=2cos3+isin32cos4+isin4=22cos3−4+isin3−4=2cos12+isin12


Finally, de Moivre's formula gives


1+i1+i312=212cos1212+isin1212=22112cos+isin=26−1+i0=−64

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:1d“