Lösung 2.2:2a

Aus Online Mathematik Brückenkurs 2

Version vom 10:21, 11. Mär. 2009

The integral is a standard integral, with 5x as the argument of the cosine function. If we therefore substitute u=5x, we obtain the “correct” argument of the cosine,

0cos5xdx=udu=5x=(5x)dx=5dx=5150cosudu.

As can be seen, the variable change replaced dx by 51du and the new limits of integration become u=50=0 and u=5=5.

Now, we have a standard integral which we can easily compute,

5150cosudu=51 sinu 05=51(sin5−sin0)=51(0−0)=0.

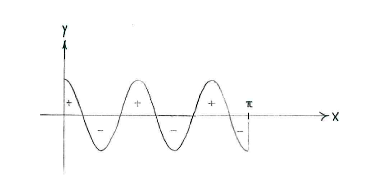
Note: If we draw the graph of y=cos5x, we see also that the area between the curve and x-axis above the x-axis is the same as the area under the x-axis.