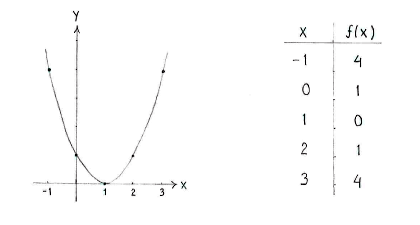Processing Math: Done

Aus Online Mathematik Brückenkurs 2

Version vom 15:26, 26. Apr. 2009 (bearbeiten) Martin (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 16:21, 26. Apr. 2009 (bearbeiten) (rückgängig) Martin (Diskussion | Beiträge) Zum nächsten Versionsunterschied →
Zeile 2:		Zeile 2:
	# stationäre Punkte, wo <math>f^{\,\prime}(x)=0</math>,		# stationäre Punkte, wo <math>f^{\,\prime}(x)=0</math>,
-	# Singuläre Punkte, wodie Funktion nicht ableitbar ist, oder	+	# Singuläre Punkte, wo die Funktion nicht ableitbar ist, oder
	# Endpunkte.		# Endpunkte.

---

Version vom 16:21, 26. Apr. 2009

Lokale Extrempunkte einer Funktion sind entweder:

1. stationäre Punkte, wo f(x)=0,
2. Singuläre Punkte, wo die Funktion nicht ableitbar ist, oder
3. Endpunkte.

Wir untersuchen alle drei Fälle.

1. Die Ableitung von f(x) ist

   f(x)=2x−2

   und ist null wenn 2x−2=0, also wenn x=1.
2. Nachdem die Funktion ein Polynom ist, ist sie überall ableitbar.
3. Die Funktion ist überall definiert, und also hat unser Intervall keine Endpunkte.

Also sind alle lokalen Extrempunkte auch stationäre Punkte, und also ist x=1 der einziger Punkt der ein Extrempunkt sein könnte. Wir untersuchen ob der Punkt ein Extrempunkt ist, mit einer Vorzeichentabelle.

x		1
f(x)	−	0	+
f(x)		0

Nachdem die Ableitung lings von x=1 negativ ist, und rechts von x=1 positiv ist, ist x=1 ein lokales Minima.

Berechnen wir zusätzlich den Funktionswert in einigen Punkten, können wir die Funktion zeichnen.