Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 2.1:1d

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Zeile 8: Zeile 8:
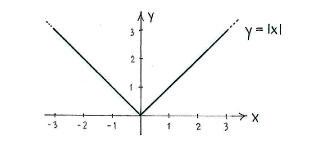
Zeichnen wir den Graph von <math>y=|x|</math>, besteht er aus zwei Teilen. Für
Zeichnen wir den Graph von <math>y=|x|</math>, besteht er aus zwei Teilen. Für
<math>x\ge 0</math> ist <math>y=x</math> und für <math>x\le 0</math> ist
<math>x\ge 0</math> ist <math>y=x</math> und für <math>x\le 0</math> ist
-
<math>y=-x\,</math>.
+
<math>y=-x\,.</math>
[[Image:2_1_1_d1.gif|center]]
[[Image:2_1_1_d1.gif|center]]

Version vom 07:48, 21. Aug. 2009

Die Betragsfunktion x returniert den Betrag von x, nimmt also das Vorzeichen von x weg. Zum Beispiel ist

−5=5, 3=3 und −=.

Für positive x ändert die Betragsfunktion nichts, da x=x, während die Betragsfunktion für negative x das Vorzeichen von x, d.h. x=−x ändert.

Zeichnen wir den Graph von y=x, besteht er aus zwei Teilen. Für x0 ist y=x und für x0 ist y=−x

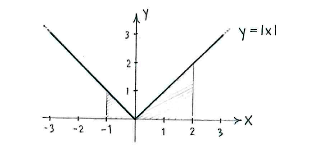
Daher ist das Integral die Fläche unter der Funktion y=x zwischen x=−1 und x=2.

Da das Gebiet aus zwei Dreiecken besteht, erhalten wir

2−1xdx=2111+2122=25. 
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1d“