Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 1.1:4

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Aktuelle Version (13:08, 21. Aug. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 4 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
If we write the equation of the tangent as
+
Wir schreiben die Tangente als
-
{{Abgesetzte Formel||<math>y=kx+m</math>}}
+
{{Abgesetzte Formel||<math>y=kx+m</math>.}}
-
we know that the tangent's slope ''k'' is equal to the derivative of <math>y = x^2</math> at the point <math>x=1\,</math>, and since <math>y^{\,\prime} = 2x\,</math>, so
+
Wir wissen, dass die Steigung ''k'' der Tangente die Ableitung von <math>y = x^2</math> im Punkt <math>x=1\,</math> ist, da <math>y^{\,\prime} = 2x\,</math>.
-
{{Abgesetzte Formel||<math>k = y^{\,\prime}(1) = 2\cdot 1 = 2\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>k = y^{\,\prime}(1) = 2\cdot 1 = 2\,\textrm{}</math>}}
-
We can determine the constant ''m'' with the condition that the tangent should go through the grazing point (1,1), i.e. the point (1,1) should satisfy the equation of the tangent
+
Wir bestimmen die Konstante ''m'' durch die Bedingung, dass die Tangente durch den Punkt (1,1) geht.
{{Abgesetzte Formel||<math>1 = 2\cdot 1 + m</math>}}
{{Abgesetzte Formel||<math>1 = 2\cdot 1 + m</math>}}
-
which gives that <math>m=-1</math>.
+
Also ist <math>m=-1</math>.
[[Image:1_1_4_1.gif|center]]
[[Image:1_1_4_1.gif|center]]
-
The normal to the curve <math>y=x^2</math> at the point (1,1) is the straight line which is perpendicular to the tangent at the same point.
+
Die Normale zu <math>y=x^2</math> im Punkt (1,1) steht senkrecht auf der Tangente im selben Punkt.
-
Because two straight lines which are perpendicular to each other have slopes which satisfy <math>k_{1}\cdot k_{2} = -1\,</math>, the normal must have a slope which is equal to
+
Nachdem zwei senkrechte Geraden <math>k_{1}\cdot k_{2} = -1\,</math> erfüllen, hat die Normale die Steigung
{{Abgesetzte Formel||<math>-\frac{1}{k} = -\frac{1}{2}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>-\frac{1}{k} = -\frac{1}{2}\,\textrm{.}</math>}}
-
The equation of the normal can therefore be written as
+
Und daher ist die Normale
-
{{Abgesetzte Formel||<math>y=-\frac{1}{2}x+n</math>}}
+
{{Abgesetzte Formel||<math>y=-\frac{1}{2}x+n</math>.}}
-
where ''n'' is some constant.
+
Um ''n'' zu bestimmen, verwenden wir die Bedingung, dass die Normale durch den Punkt (1,1) geht.
-
Since the normal must pass through the line (1,1), we can determine the constant ''n'' if we substitute the point into the equation of the normal,
+
{{Abgesetzte Formel||<math>1=-\frac{1}{2}\cdot 1 + n</math>}}
-
{{Abgesetzte Formel||<math>1=-\frac{1}{2}\cdot + n</math>}}
+
Wir erhalten <math>n=\tfrac{3}{2}\,</math>.
-
 
+
-
and this gives <math>n=\tfrac{3}{2}\,</math>.
+
[[Image:1_1_4-3(3).gif|center]]
[[Image:1_1_4-3(3).gif|center]]

Aktuelle Version

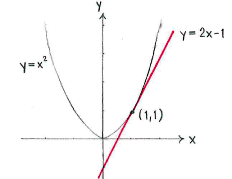
Wir schreiben die Tangente als

y=kx+m.

Wir wissen, dass die Steigung k der Tangente die Ableitung von y=x2 im Punkt x=1 ist, da y=2x.

k=y(1)=21=2

Wir bestimmen die Konstante m durch die Bedingung, dass die Tangente durch den Punkt (1,1) geht.

1=21+m

Also ist m=−1.

Die Normale zu y=x2 im Punkt (1,1) steht senkrecht auf der Tangente im selben Punkt.

Nachdem zwei senkrechte Geraden k1k2=−1 erfüllen, hat die Normale die Steigung

−k1=−21.

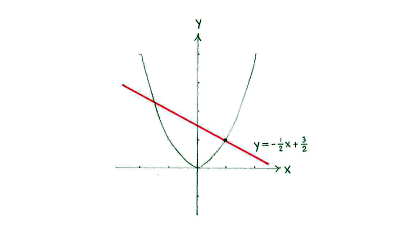
Und daher ist die Normale

y=−21x+n.

Um n zu bestimmen, verwenden wir die Bedingung, dass die Normale durch den Punkt (1,1) geht.

1=−211+n

Wir erhalten n=23.

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.1:4“