Lösung 3.3:2b
Aus Online Mathematik Brückenkurs 2
| Zeile 10: | Zeile 10: | ||
{{Abgesetzte Formel||<math>r^3(\cos 3\alpha + i\sin 3\alpha) = 1\,(\cos\pi + i\sin\pi)\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>r^3(\cos 3\alpha + i\sin 3\alpha) = 1\,(\cos\pi + i\sin\pi)\,\textrm{.}</math>}} | ||
| - | Die beiden Seiten sind gleich, wenn die Beträge gleich sind und die Argumente sich nur | + | Die beiden Seiten sind gleich, wenn die Beträge gleich sind und die Argumente sich nur durch ein Vielfaches von <math>2\pi</math> unterscheiden |
{{Abgesetzte Formel||<math>\left\{\begin{align} | {{Abgesetzte Formel||<math>\left\{\begin{align} | ||
Version vom 12:02, 3. Sep. 2009
Wir bringen zuerst alle Zahlen in Polarform.
| \displaystyle \begin{align}
z &= r(\cos\alpha + i\sin\alpha)\,\\[5pt] -1 &= 1\,(\cos\pi + i\sin\pi)\, \end{align} |
Mit dem Moivreschen Satz erhalten wir die Gleichung
| \displaystyle r^3(\cos 3\alpha + i\sin 3\alpha) = 1\,(\cos\pi + i\sin\pi)\,\textrm{.} |
Die beiden Seiten sind gleich, wenn die Beträge gleich sind und die Argumente sich nur durch ein Vielfaches von \displaystyle 2\pi unterscheiden
| \displaystyle \left\{\begin{align}
r^3 &= 1\,,\\[5pt] 3\alpha &= \pi + 2n\pi\,,\quad\text{(n ist eine beliebige natürliche Zahl).} \end{align}\right. |
Dadurch erhalten wir
| \displaystyle \left\{\begin{align}
r &= 1\,,\\[5pt] \alpha &= \frac{\pi}{3}+\frac{2n\pi}{3}\,,\quad\text{(n ist eine beliebige natürliche Zahl).} \end{align}\right. |
Für jede dritte ganze Zahl \displaystyle n, erhalten wir dieselbe Lösung, also hat die Gleichung nur 3 Lösungen - eine für \displaystyle n=0, für \displaystyle n=1 und für \displaystyle n=2).
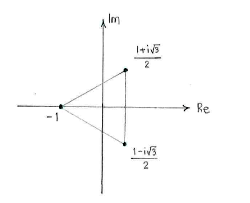
| \displaystyle z=\left\{\begin{align}
&1\cdot \Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\\[5pt] &1\cdot \Bigl(\cos\pi + i\sin\pi\Bigr)\\[5pt] &1\cdot \Bigl(\cos\frac{5\pi}{3} + i\sin\frac{5\pi}{3}\Bigr) \end{align}\right. = \left\{\begin{align} &\frac{1+i\sqrt{3}}{2}\,,\\[5pt] &-1\vphantom{\bigl(}\,,\\[5pt] &\frac{1-i\sqrt{3}}{2}\,\textrm{.} \end{align} \right. |
Wir sehen, dass die Wurzeln ein symmetrisches Polygon bilden. In diesem Fall erhalten wir ein Dreieck, da wir 3 Lösungen haben.