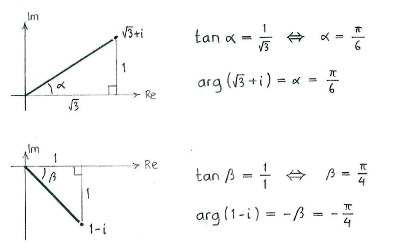Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 3.2:5c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (17:44, 14. Sep. 2009) (bearbeiten) (rückgängig)
(nur sprachliche Aenderung)
 
(Der Versionsvergleich bezieht 5 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
Geometrically, the multiplication of two complex numbers means that there magnitudes are multiplied and their arguments are added. The product
+
Geometrisch ist das Argument von einem Produkt die Summe der Argumente der beiden Faktoren bzw. Terme. Also ist das Argument von <math>(\sqrt{3}+i)(1-i)</math> die Summe der Argumente von <math>\sqrt{3}+i</math> und <math>1-i</math>,
-
<math>\left( \sqrt{3}+i \right)\left( 1-i \right)</math>
+
-
therefore has an argument which is the sum of the argument for the
+
-
<math>\sqrt{3}+i</math>
+
-
and
+
-
<math>1-i</math>, i.e.
+
-
 
+
-
 
+
-
<math>\arg \left( \left( \sqrt{3}+i \right)\left( 1-i \right) \right)=\arg \left( \sqrt{3}+i \right)+\arg \left( 1-i \right)</math>
+
-
 
+
-
 
+
-
By drawing the factors in the complex plane, we can determine relatively easily the argument using simple trigonometry:
+
 +
{{Abgesetzte Formel||<math>\arg \bigl((\sqrt{3}+i)(1-i)\bigr) = \arg (\sqrt{3}+i) + \arg (1-i)\,\textrm{.}</math>}}
 +
Indem wir die Faktoren in der komplexen Zahlenebene einzeichnen, können wir deren Argumente durch Trigonometrie berechnen.
[[Image:3_2_5_c.gif|center]]
[[Image:3_2_5_c.gif|center]]
 +
(Da <math>1-i</math> im vierten Quadrant liegt, ist das Argument
 +
<math>-\beta</math> und nicht <math>\beta</math>.)
-
(Because
+
Daher erhalten wir,
-
<math>1-i</math>
+
-
lies in the fourth quadrant, the argument equals
+
-
<math>-\beta </math>
+
-
and not
+
-
<math>\beta </math>.)
+
-
 
+
-
Hence,
+
-
 
+
-
 
+
-
<math>\begin{align}
+
-
& \arg \left( \left( \sqrt{3}+i \right)\left( 1-i \right) \right)=\arg \left( \sqrt{3}+i \right)+\arg \left( 1-i \right) \\
+
-
& =\frac{\pi }{6}-\frac{\pi }{4}=-\frac{\pi }{12} \\
+
-
\end{align}</math>
+
 +
{{Abgesetzte Formel||<math>\arg \bigl((\sqrt{3}+i)(1-i)\bigr) = \arg (\sqrt{3}+i) + \arg (1-i) = \frac{\pi}{6} - \frac{\pi}{4} = -\frac{\pi}{12}\,\textrm{.}</math>}}
-
NOTE: if you prefer to give the argument between
 
-
<math>0</math>
 
-
and
 
-
<math>2\pi </math>, then the answer is
 
 +
Hinweis: Wenn wir das Argument als einen Winkel zwischen <math>0</math> und <math>2\pi </math> schreiben, ist die Antwort
-
<math>-\frac{\pi }{12}+2\pi =\frac{-\pi +24\pi }{12}=\frac{23\pi }{12}</math>
+
{{Abgesetzte Formel||<math>-\frac{\pi}{12}+2\pi = \frac{-\pi+24\pi}{12} = \frac{23\pi}{12}\,\textrm{.}</math>}}

Aktuelle Version

Geometrisch ist das Argument von einem Produkt die Summe der Argumente der beiden Faktoren bzw. Terme. Also ist das Argument von (3+i)(1−i)  die Summe der Argumente von 3+i  und 1−i,

arg(3+i)(1−i)=arg(3+i)+arg(1−i). 

Indem wir die Faktoren in der komplexen Zahlenebene einzeichnen, können wir deren Argumente durch Trigonometrie berechnen.

(Da 1−i im vierten Quadrant liegt, ist das Argument − und nicht .)

Daher erhalten wir,

arg(3+i)(1−i)=arg(3+i)+arg(1−i)=6−4=−12. 


Hinweis: Wenn wir das Argument als einen Winkel zwischen 0 und 2 schreiben, ist die Antwort

−12+2=12−+24=1223.
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:5c“