Processing Math: 94%
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 1.3:6

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 1.3:6 moved to Solution 1.3:6: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
If we call the radius of the metal can
-
<center> [[Image:1_3_6-1(4).gif]] </center>
+
<math>r</math>
-
{{NAVCONTENT_STOP}}
+
and its height
-
{{NAVCONTENT_START}}
+
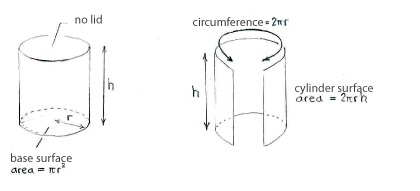
<math>h</math>, then we can determine the can's volume and area by using the figures below.
-
<center> [[Image:1_3_6-2(4).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
Volume = (area of the base). (height)
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Image:1_3_6-3(4).gif]] </center>
+
<math>=\pi r^{2}h</math>
-
{{NAVCONTENT_STOP}}
+
 
-
{{NAVCONTENT_START}}
+
Area= (area of the base)+(area of the cylindrical surface)
-
<center> [[Image:1_3_6-4(4).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
<math>=\pi r^{2}+2\pi h</math>
 +
 
[[Image:1_3_6_1.gif|center]]
[[Image:1_3_6_1.gif|center]]
 +
 +
 +
The problem can then be formulated as: minimise the can's area,
 +
<math>A=\pi r^{2}+2\pi h</math>, whilst at the same time keeping the volume,
 +
<math>V=\pi r^{2}h</math>, constant.
 +
 +
From the formula for the volume, we can make
 +
<math>h</math>
 +
the subject,
 +
 +
 +
<math>h=\frac{V}{\pi r^{2}}</math>
 +
 +
 +
and express the area solely in terms of the radius,
 +
<math>r</math>:
 +
 +
 +
<math>A=\pi r^{2}+2\pi r\bullet \frac{V}{\pi r^{2}}=\pi r^{2}+\frac{2V}{r}</math>
 +
 +
 +
The minimisation problem is then:
 +
 +
to minimise the area
 +
<math>A\left( r \right)=\pi r^{2}+\frac{2V}{r}</math>
 +
A(r)=..., when
 +
<math>r>0</math>.
 +
 +
The area function
 +
<math>A\left( r \right)</math>
 +
is differentiable for all
 +
<math>r>0</math>
 +
and the region of definition
 +
<math>r>0</math>
 +
has no endpoints
 +
(
 +
<math>r=0\text{ }</math>
 +
does not satisfy
 +
<math>r>0</math>
 +
), so the function can only assume extreme values at critical points.
 +
 +
The derivative is given by
 +
 +
 +
<math>{A}'\left( r \right)=2\pi r-\frac{2V}{r^{2}}</math>,
 +
 +
and if we set the derivative equal to zero, so as to obtain the critical points, we get
 +
 +
<math>\begin{align}
 +
& 2\pi r-\frac{2V}{r^{2}}=0\quad \Leftrightarrow \quad 2\pi r=\frac{2V}{r^{2}} \\
 +
& \Leftrightarrow \quad r^{3}=\frac{V}{\pi }\quad \Leftrightarrow \quad r=\sqrt[3]{\frac{V}{\pi }} \\
 +
\end{align}</math>
 +
 +
 +
 +
For this value of
 +
<math>r</math>, the second derivative,
 +
 +
 +
<math>{A}''\left( r \right)=2\pi +\frac{4V}{r^{3}}</math>,
 +
has the value
 +
 +
 +
<math>{A}''\left( \sqrt[3]{\frac{V}{\pi }} \right)=2\pi +\frac{4V}{\frac{V}{\pi }}=6\pi >0</math>,
 +
 +
which shows that
 +
<math>r=\sqrt[3]{{V}/{\pi }\;}</math>
 +
is a local minimum.
 +
 +
Because the region of definition,
 +
<math>r>0</math>, is open (the endpoint
 +
<math>r=0\text{ }</math>
 +
is not included) and unlimited, we cannot directly say that the area is least when
 +
<math>r=\sqrt[3]{{V}/{\pi }\;}</math>; it could be the case that area becomes smaller when
 +
<math>r\to 0</math>
 +
or
 +
<math>r\to \infty </math>. In this case, however, the area increases without bound as
 +
<math>r\to 0</math>
 +
or
 +
<math>r\to \infty </math>, so
 +
<math>r=\sqrt[3]{{V}/{\pi }\;}</math>
 +
really is a global minimum.
 +
 +
The metal can has the least area for a given volume
 +
<math>V</math>
 +
when
 +
 +
 +
<math>r=\sqrt[3]{{V}/{\pi }\;}</math>, and
 +
 +
<math>h=\frac{V}{\pi r^{2}}=\frac{V}{\pi }\left( \frac{V}{\pi } \right)^{-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{1-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{{1}/{3}\;}=\sqrt[3]{\frac{V}{\pi }}</math>

Version vom 13:35, 16. Okt. 2008

If we call the radius of the metal can r and its height h, then we can determine the can's volume and area by using the figures below.

Volume = (area of the base). (height)

=r2h

Area= (area of the base)+(area of the cylindrical surface)

=r2+2h



The problem can then be formulated as: minimise the can's area, A=r2+2h, whilst at the same time keeping the volume, V=r2h, constant.

From the formula for the volume, we can make h the subject,


h=Vr2


and express the area solely in terms of the radius, r:


A=r2+2rVr2=r2+r2V


The minimisation problem is then:

to minimise the area Ar=r2+r2V  A(r)=..., when r0.

The area function Ar  is differentiable for all r0 and the region of definition r0 has no endpoints ( r=0 does not satisfy r0 ), so the function can only assume extreme values at critical points.

The derivative is given by


Ar=2r−r22V ,

and if we set the derivative equal to zero, so as to obtain the critical points, we get

2r−r22V=02r=r22Vr3=Vr=3V 


For this value of r, the second derivative,


Ar=2+r34V , has the value


A3V=2+V4V=60 ,

which shows that r=3V  is a local minimum.

Because the region of definition, r0, is open (the endpoint r=0 is not included) and unlimited, we cannot directly say that the area is least when r=3V ; it could be the case that area becomes smaller when r0 or r. In this case, however, the area increases without bound as r0 or r, so r=3V  really is a global minimum.

The metal can has the least area for a given volume V when


\displaystyle r=\sqrt[3]{{V}/{\pi }\;}, and

\displaystyle h=\frac{V}{\pi r^{2}}=\frac{V}{\pi }\left( \frac{V}{\pi } \right)^{-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{1-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{{1}/{3}\;}=\sqrt[3]{\frac{V}{\pi }}

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:6“