Lösung 1.1:5
Aus Online Mathematik Brückenkurs 2
| Zeile 1: | Zeile 1: | ||
| - | Wir nehmen an dass die Tangente(n) die Kurve im Punkt <math>(x_0,y_0)</math> | + | Wir nehmen an, dass die Tangente(n) die Kurve im Punkt <math>(x_0,y_0)</math> berührt. Dieser Punkt liegt natürlich auf der Kurve, erfüllt also |
{{Abgesetzte Formel||<math>y_0 = -x_0^2\,\textrm{.}</math>|(1)}} | {{Abgesetzte Formel||<math>y_0 = -x_0^2\,\textrm{.}</math>|(1)}} | ||
| - | Schreiben wir die Tangente | + | Schreiben wir die Tangente als <math>y=kx+m</math>, ist die Steigung ''k'' dasselbe wie die Ableitung, <math>y^{\,\prime} = -2x</math>, im Punkt <math>x=x_0</math>, |
{{Abgesetzte Formel||<math>k = -2x_0\,\textrm{.}</math>|(2)}} | {{Abgesetzte Formel||<math>k = -2x_0\,\textrm{.}</math>|(2)}} | ||
| - | Die | + | Die Bedingung, dass die Tangente durch den Punkt <math>(x_0,y_0)</math> geht, gibt |
{{Abgesetzte Formel||<math>y_{0} = k\cdot x_0 + m\,\textrm{.}</math>|(3)}} | {{Abgesetzte Formel||<math>y_{0} = k\cdot x_0 + m\,\textrm{.}</math>|(3)}} | ||
| - | + | Die Bedingung dass die Tangente durch den Punkt (1,1) geht, gibt | |
{{Abgesetzte Formel||<math>1 = k\cdot 1 + m\,\textrm{.}</math>|(4)}} | {{Abgesetzte Formel||<math>1 = k\cdot 1 + m\,\textrm{.}</math>|(4)}} | ||
| Zeile 17: | Zeile 17: | ||
Die Gleichungen (1)-(4) sind ein System von Gleichungen mit den unbekannten <math>x_0</math>, <math>y_{0}</math>, <math>k</math> und <math>m</math>. | Die Gleichungen (1)-(4) sind ein System von Gleichungen mit den unbekannten <math>x_0</math>, <math>y_{0}</math>, <math>k</math> und <math>m</math>. | ||
| - | + | Da wir <math>x_0</math> und <math>y_0</math> suchen, eliminieren wir zuerst ''k'' und ''m'', | |
| - | + | Aus der Gleichung (2) folgt, dass <math>k = -2 x_0</math> Das in Gleichung (4) eingesetzt, liefert | |
{{Abgesetzte Formel||<math>1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.}</math>}} | ||
| - | Jetzt haben wir ''k'', und ''m'' in Termen von <math>x_0</math> und <math>y_0</math> ausgedrückt, und | + | Jetzt haben wir ''k'', und ''m'' in Termen von <math>x_0</math> und <math>y_0</math> ausgedrückt, und Gleichung (3) hat nun nur <math>x_0</math-> |
und <math>y_0</math>-Terme, | und <math>y_0</math>-Terme, | ||
Version vom 12:08, 7. Aug. 2009
Wir nehmen an, dass die Tangente(n) die Kurve im Punkt \displaystyle (x_0,y_0) berührt. Dieser Punkt liegt natürlich auf der Kurve, erfüllt also
| \displaystyle y_0 = -x_0^2\,\textrm{.} | (1) |
Schreiben wir die Tangente als \displaystyle y=kx+m, ist die Steigung k dasselbe wie die Ableitung, \displaystyle y^{\,\prime} = -2x, im Punkt \displaystyle x=x_0,
| \displaystyle k = -2x_0\,\textrm{.} | (2) |
Die Bedingung, dass die Tangente durch den Punkt \displaystyle (x_0,y_0) geht, gibt
| \displaystyle y_{0} = k\cdot x_0 + m\,\textrm{.} | (3) |
Die Bedingung dass die Tangente durch den Punkt (1,1) geht, gibt
| \displaystyle 1 = k\cdot 1 + m\,\textrm{.} | (4) |
Die Gleichungen (1)-(4) sind ein System von Gleichungen mit den unbekannten \displaystyle x_0, \displaystyle y_{0}, \displaystyle k und \displaystyle m.
Da wir \displaystyle x_0 und \displaystyle y_0 suchen, eliminieren wir zuerst k und m,
Aus der Gleichung (2) folgt, dass \displaystyle k = -2 x_0 Das in Gleichung (4) eingesetzt, liefert
| \displaystyle 1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.} |
Jetzt haben wir k, und m in Termen von \displaystyle x_0 und \displaystyle y_0 ausgedrückt, und Gleichung (3) hat nun nur \displaystyle x_0 und -Terme,
| \displaystyle y_0 = -2x_0^2 + 2x_0 + 1\,\textrm{.} | (3') |
Diese Gleichung, und die Gleichung (1), bilden ein Gleichungssystem für \displaystyle x_0 und \displaystyle y_0,
| \displaystyle \left\{\begin{align}
y_{0} &= -x_0^{2}\,,\\[5pt] y_{0} &= -2x_0^2 + 2x_0 + 1\,\textrm{.} \end{align}\right. |
Substituieren wir (1) in (3), erhalten wir eine Gleichung mit nur \displaystyle x_0,
| \displaystyle -x_0^2 = -2x_0^2 + 2x_0 + 1\,, |
also
| \displaystyle x_0^2 - 2x_0 - 1 = 0\,\textrm{.} |
Diese Quadratische Gleichung hat die Lösungen
| \displaystyle x_0 = 1-\sqrt{2}\qquad\text{and}\qquad x_0 = 1+\sqrt{2}\,\textrm{.} |
Durch die Gleichung (1) erhalten wir den entsprechenden y-Wert,
| \displaystyle y_0 = -3+2\sqrt{2}\qquad\text{and}\qquad y_0 = -3-2\sqrt{2}\,\textrm{.} |
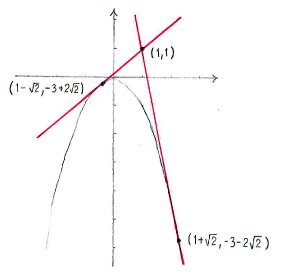
Also erhalten wir die Punkte \displaystyle (1-\sqrt{2},-3+2\sqrt{2}) und \displaystyle (1+\sqrt{2},-3-2\sqrt{2})\,.