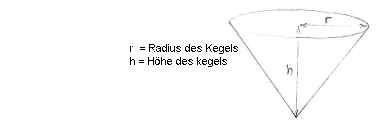Processing Math: 41%
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 1.3:7

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (18:10, 9. Sep. 2009) (bearbeiten) (rückgängig)
 
Zeile 60: Zeile 60:
::Maximiere <math>V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\ </math> , für <math>0\le x\le 1\,</math>.
::Maximiere <math>V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\ </math> , für <math>0\le x\le 1\,</math>.
-
Wenn <math>x=0</math> oder <math>x=1</math> ist, ist das Volumen null. Weil die Funktion überall (außer in <math>x=1</math>) differenzierbar ist, nimmt das Volumen sein Maximum in einem stationären Punkt an.
+
Wenn <math>x=0</math> oder <math>x=1</math> ist, ist das Volumen null. Weil die Funktion überall (außer in <math>x=1</math>) differenzierbar ist, nimmt das Volumen sein Maximum an einer stationären Stelle an.
Wir leiten die Funktion ab
Wir leiten die Funktion ab
Zeile 74: Zeile 74:
\end{align}</math>}}
\end{align}</math>}}
-
Die Ableitung ist null, wenn <math>x=0</math> (dies ist ein Randpunkt) oder wenn <math>2-3x^2=0</math> ist, also wenn <math>x=\sqrt{2/3}\,</math>. (Der Punkt <math>x=-\sqrt{2/3}</math> liegt außerhalb des Gebietes <math>0\le x\le 1</math>.)
+
Die Ableitung ist null, wenn <math>x=0</math> (dies ist ein Randpunkt) oder wenn <math>2-3x^2=0</math> ist, also wenn <math>x=\sqrt{2/3}\,</math>. (Die Stelle <math>x=-\sqrt{2/3}</math> liegt außerhalb des Gebietes <math>0\le x\le 1</math>.)
Durch eine Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren
Durch eine Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren
Zeile 137: Zeile 137:
|}
|}
-
Wir sehen hier, dass <math>x=\sqrt{2/3}</math> ein globales Maximum ist. <math>x = \sqrt{2/3}</math> entspricht dem Winkel <math>\alpha</math>:
+
Wir sehen hier, dass die Funktion an der Stelle <math>x=\sqrt{2/3}</math> ein globales Maximum hat. <math>x = \sqrt{2/3}</math> entspricht dem Winkel <math>\alpha</math>:
{{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ </math>}}
{{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ </math>}}

Aktuelle Version

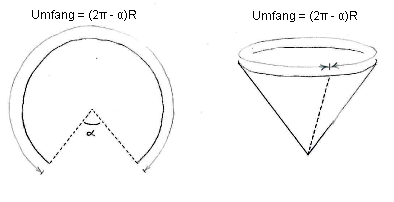
Wie der Kegel gebaut wird, ist hier illustriert.

Da wir das Volumen des Kegels maximieren wollen, betrachten wir nun die Abmessungen Kegels.

Mit diesen Abmessungen ist das Volumen des Kegels

V=31(Fläche des Kreises)(Höhe)=31r2h.

Wir müssen jetzt den Radius r und die Höhe h durch den Winkel ausdrücken, sodass wir das Volumen V als Funktion von schreiben können.

Schneiden wir einen Kreissektor mit dem Winkel aus dem Kreis, ist der Umfang des übriggebliebenen Kreissegments (2−)R, wobei R der ursprüngliche Radius ist.

Der Umfang des oberen Kreises ist aber auch 2r, also haben wir

2r=(2−)Rr=22−R.

Jetzt haben wir den neuen Radius r als Funktion des Winkels und des ursprünglichen Radius R ausgedrückt.

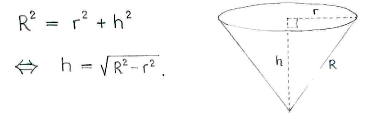
Um die Höhe zu bestimmen, benutzen wir den Satz des Pythagoras.

Also haben wir

h=R2−22−R2=R2−22−2R2=R1−22−2.

Jetzt haben wir den Radius r und die Höhe h als Funktionen von und R geschrieben. Das Volumen des Kegels ist also

V=31r2h=3122−R2R1−22−2=31R322−21−22−2.

Unser Problem ist jetzt:

Maximiere V()=31R322−21−22−2 , wo 02.

Bevor wir anfangen die Funktion abzuleiten, sehen wir, dass der Winkel nur in (2−)2-Termen auftritt. Um das Problem zu vereinfachen, können wir das Volumen genauso in Bezug auf die Variable x=(2−)2 maximieren.

Maximiere V(x)=31R3x21−x2   , für 0x1.

Wenn x=0 oder x=1 ist, ist das Volumen null. Weil die Funktion überall (außer in x=1) differenzierbar ist, nimmt das Volumen sein Maximum an einer stationären Stelle an.

Wir leiten die Funktion ab

V(x)=31R32x1−x2+31R3x2121−x2(−2x)

und vereinfachen den Ausdruck, indem wir so viele Faktoren wir möglich herausziehen.

V(x)=32R3x1−x2−31R3x311−x2=31R3x1−x22(1−x2)−x2=31R3x1−x2(2−3x2)

Die Ableitung ist null, wenn \displaystyle x=0 (dies ist ein Randpunkt) oder wenn \displaystyle 2-3x^2=0 ist, also wenn \displaystyle x=\sqrt{2/3}\,. (Die Stelle \displaystyle x=-\sqrt{2/3} liegt außerhalb des Gebietes \displaystyle 0\le x\le 1.)

Durch eine Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren

\displaystyle x \displaystyle 0 \displaystyle \sqrt{\tfrac{2}{3}} \displaystyle 1
\displaystyle x \displaystyle 0 \displaystyle + \displaystyle + \displaystyle + \displaystyle +
\displaystyle \sqrt{1-x^2} \displaystyle + \displaystyle + \displaystyle + \displaystyle + \displaystyle 0
\displaystyle 2-3x^2 \displaystyle + \displaystyle + \displaystyle 0 \displaystyle - \displaystyle -


und erhalten dadurch das Vorzeichen der Ableitung selbst.


\displaystyle x \displaystyle 0 \displaystyle \sqrt{\tfrac{2}{3}} \displaystyle 1
\displaystyle V'(x) \displaystyle 0 \displaystyle + \displaystyle 0 \displaystyle -  
\displaystyle V(x) \displaystyle 0 \displaystyle \nearrow \displaystyle \tfrac{4}{9\sqrt{3}}\pi R^3 \displaystyle \searrow \displaystyle 0

Wir sehen hier, dass die Funktion an der Stelle \displaystyle x=\sqrt{2/3} ein globales Maximum hat. \displaystyle x = \sqrt{2/3} entspricht dem Winkel \displaystyle \alpha:

\displaystyle \sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:7“