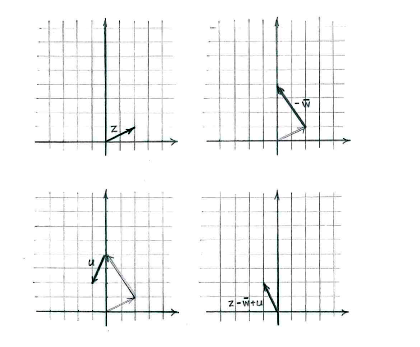
Berechnen wir den Punkt, erhalten wir direkt
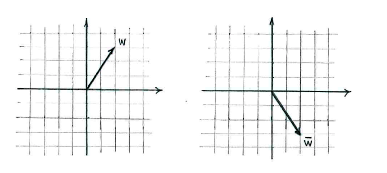
Um den Vektor w geometrisch zu deuten, müssen wir wissen, dass die komplexe Konjugation von w eine Spiegelung an der reellen Achse ist, nachdem der Imaginärteil durch die Kunjugation ihr Vorzeichen tauscht.
Dadurch erhalten wir den Ausdruck einfach:
+u=(2+i)−(2−3i)+(−1−2i)=2−2−1+(1+3−2)i=−1+2i.
