Processing Math: Done

Aus Online Mathematik Brückenkurs 2

The The equation z3=−1 is a so-called binomial equation, which we solve by writing both sides in polar form. We have

z=rcos+isin−1=1cos+isin 

and, with the help of de Moivre's formula, the equation becomes

r3cos3+isin3=1cos+isin 

Both sides are equal when their magnitudes are equal and the arguments differ by a multiple of 2,

r3=13=+2nn an arbitrary integer  

which gives that

r=1=3+32nn an arbitrary integer  

For every third integer n, the solution formula gives in principal the same value for the argument (the difference is a multiple of 2), so the equation has in reality three solutions (for n=0 1 and 2):

z=1cos3+isin31cos+isin1cos35+isin35=21+i3−121−i3

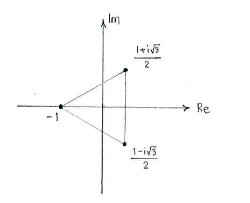
We obtain the typical behaviour that the solutions are corner points in a regular polygon (a triangle in this case because the degree of the equation is 3).