Lösung 1.3:2b
Aus Online Mathematik Brückenkurs 2
In order to determine the function's extreme points, we investigate three types of points,
- critical points, i.e. where \displaystyle f^{\,\prime}(x)=0,
- points where the function is not differentiable, and
- endpoints of the interval of definition.
In our case, we have that:
- The derivative of \displaystyle f(x) is given by
and becomes zero when \displaystyle x=3/2\,.\displaystyle f^{\,\prime}(x) = 3-2x - The function is a polynomial, and is therefore differentiable everywhere.
- The function is defined for all x, and therefore the interval of definition has no endpoints.
There is thus just one point \displaystyle x=3/2\,, where the function possibly has an extreme point.
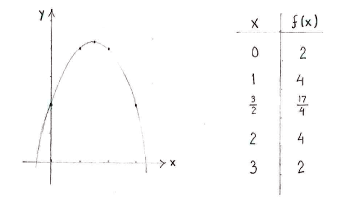
If we write down a sign table for the derivative, we see that \displaystyle x=3/2 is a local maximum.
| \displaystyle x | \displaystyle \tfrac{3}{2} | ||
| \displaystyle f^{\,\prime}(x) | \displaystyle + | \displaystyle 0 | \displaystyle - |
| \displaystyle f(x) | \displaystyle \nearrow | \displaystyle \tfrac{17}{4} | \displaystyle \searrow |
Because the function is given by a second-degree expression, its graph is a parabola with a maximum at \displaystyle (3/2, 17/4) and we can draw it with the help of a few couple of points.