Lösung 3.3:2b
Aus Online Mathematik Brückenkurs 2
The equation \displaystyle z^3=-1 is a so-called binomial equation, which we solve by writing both sides in polar form. We have
| \displaystyle \begin{align}
z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] -1 &= 1\,(\cos\pi + i\sin\pi)\,, \end{align} |
and, with the help of de Moivre's formula, the equation becomes
| \displaystyle r^3(\cos 3\alpha + i\sin 3\alpha) = 1\,(\cos\pi + i\sin\pi)\,\textrm{.} |
Both sides are equal when their magnitudes are equal and the arguments differ by a multiple of \displaystyle 2\pi,
| \displaystyle \left\{\begin{align}
r^3 &= 1\,,\\[5pt] 3\alpha &= \pi + 2n\pi\,,\quad\text{(n is an arbitrary integer),} \end{align}\right. |
which gives that
| \displaystyle \left\{\begin{align}
r &= 1\,\\[5pt] \alpha &= \frac{\pi}{3}+\frac{2n\pi}{3}\quad\text{(n is an arbitrary integer).} \end{align}\right. |
For every third integer \displaystyle n, the solution formula gives in principal the same value for the argument (the difference is a multiple of \displaystyle 2\pi), so the equation has in reality three solutions (for \displaystyle n=0, \displaystyle 1 and \displaystyle \text{2}),
| \displaystyle z=\left\{\begin{align}
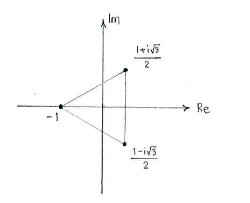
&1\cdot \Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\\[5pt] &1\cdot \Bigl(\cos\pi + i\sin\pi\Bigr)\\[5pt] &1\cdot \Bigl(\cos\frac{5\pi}{3} + i\sin\frac{5\pi}{3}\Bigr) \end{align}\right. = \left\{\begin{align} &\frac{1+i\sqrt{3}}{2}\,,\\[5pt] &-1\vphantom{\bigl(}\,,\\[5pt] &\frac{1-i\sqrt{3}}{2}\,\textrm{.} \end{align} \right. |
We obtain the typical behaviour that the solutions are corner points in a regular polygon (a triangle in this case because the degree of the equation is 3.