Lösung 1.3:6

Aus Online Mathematik Brückenkurs 2

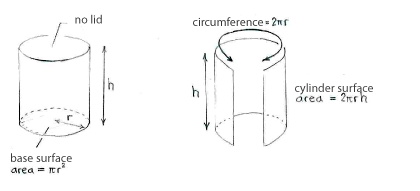
Wir benennen den Radius der Tasse r und die Höhe h. Der Volumen ist

VolumeFläche=(Fläche der Basis)(Höhe)=r2h=(Fläche der Basis)+(Fläche des Zylinders)=r2+2rh.

Das Problem ist also; Minimiere die Fläche A=r2+2h, während der Volumen V=r2h, konstant ist.

Wir schreiben h als Funktion des Volumen,

h=Vr2

und können dadurch die Fläche als Funktion von r schreiben,

A=r2+2rVr2=r2+r2V.

Unser Problem ist dann

Minimiere die Flächea A(r)=r2+r2V, wenn r0.

Die Funktion A(r) ist für alle r0 differenzierbar, und der Bereich r0 hat keine Endpunkte (nachdem r=0 nicht r0 erfüllt), und also erscheinen Extrempunkte nur in stationären Punkten.

Die Ableitung ist

A(r)=2r−r22V

Und die Ableitung gleich null ergibt folgende Gleichung

2r−r22V=02r=r22Vr3=Vr=3V.

Die zweite Ableitung ist

A(r)=2+r34V

und hat den Wert

A3V=2+4VV=60

im stationären Punkt.

Also ist r=3V  ein lokales Minima.

Nachdem wir kein begrenztes Intervall haben, können wir nicht direkt ausschließen dass die Fläche kleiner wird wenn r0 oder wenn r. In unseren Fall wächst die Fläche aber unbegrenzt in den beiden Richtungen r0 und r, und also ist

r=3V  ein globales Minima.

Also ist die Fläche minimal wenn

rh=3Vand=Vr2=VV−23=V1−23=V13=3V.