Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 10.6

From Mechanics

Jump to: navigation, search

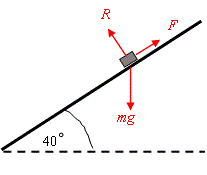
Image:10.6.gif


The figure shows the forces acting on the particle.

Assuming the particle has an acceleration a down the plane Newton´s Second Law applied down the plane gives,


mgsin40−F=ma (equation of motion)

We need to obtain F.

Resolving perpendicular to the plane the sum of the forces on the particle must be zero as the particle has no motion in that direction.

R−mgcos40=0R=mgcos40


The friction condition gives


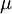F=R which gives


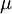F=mgcos40


Substituting in the equation of motion above

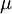mgsin40−mgcos40=ma

We can cancel the mass m in this equation giving

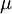gsin40−gcos40=a or

a=9.810.643−0.29.810.77==9.81(0.643−0.154)=9.810.489=4.80 ms−2

Note by waiting to substitute the values of the various quantities we minimized the amount of calculation needed. Also the result is independent of the mass of the particle as we could cancel it out.

Retrieved from "http://wiki.math.se/wikis/2009/bridgecoursemechanics/index.php/Solution_10.6"