Processing Math: Done
Solution 2.6
From Mechanics
Use the theory of gravitation equation
where,
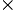 10−11 kg-1m3s-2
10−11 kg-1m3s-2
In this case
Thus
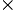 1024 kg
1024 kg
The radius of the earth is
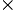 106 m
106 m
and the height of the satellite above the earth in SI units is 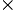 106 m
106 m
which gives
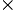 106 m
106 m
Inserting all these quantities in the gravitation equation
 13.37
13.37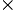 106
106 2
2 6.67
6.67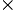 10−11
10−11
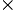
 5.98
5.98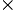 1024
1024
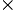 300=178.76
300=178.76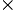 1012119.66
1012119.66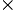 1015=0.669
1015=0.669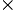 103 =669 N
103 =669 N
