4.1 Vinklar och cirklar

Förberedande kurs i matematik 1

Hoppa till: navigering, sök
       Teori          Övningar      

Innehåll:

  • Olika vinkelmått (grader, radianer och varv)
  • Pythagoras sats
  • Avståndsformeln i planet
  • Cirkelns ekvation

Lärandemål:

Efter detta avsnitt ska du ha lärt dig att:

  • Omvandla mellan grader, radianer och varv.
  • Beräkna arean och omkretsen av cirkelsektorer.
  • Känna till begreppen katet, hypotenusa och rätvinklig triangel.
  • Formulera och använda Pythagoras sats.
  • Beräkna avståndet mellan två punkter i planet.
  • Skissera cirklar med hjälp av att kvadratkomplettera deras ekvationer.
  • Känna till begreppen enhetscirkel, tangent, radie, diameter, periferi, korda och cirkelbåge.
  • Lösa geometriska problem som innehåller cirklar.

Vinkelmått

Det finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.

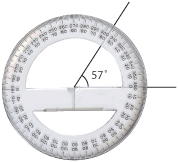
  • Grader. Om ett helt varv delas in i 360 delar, så kallas varje del 1 grad. Beteckningen för grader är \displaystyle {}^\circ.
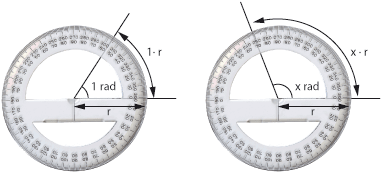
  • Radianer. Ett annat sätt att mäta vinklar är att använda längden av vinkelns cirkelbåge i förhållande till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså \displaystyle 2\pi radianer eftersom cirkelns omkrets är \displaystyle 2\pi r, där \displaystyle r är cirkelns radie.


Ett helt varv är \displaystyle 360^\circ eller \displaystyle 2\pi radianer och det gör att

\displaystyle \begin{align*} 
   &1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radianer }
            = \frac{\pi}{180}\ \mbox{ radianer,}\\
   &1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
            = \frac{180^\circ}{\pi}\,\mbox{.}
 \end{align*}

Dessa omvandlingsfaktorer kan användas för att konvertera mellan grader och radianer.

Exempel 1

  1. \displaystyle 30^\circ = 30 \cdot 1^\circ = 30 \cdot \frac{\pi}{180}\ \mbox{ radianer } = \frac{\pi}{6}\ \mbox{ radianer }
  2. \displaystyle \frac{\pi}{8}\ \mbox { radianer } = \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,) = \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} = 22{,}5^\circ

I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv.

[Image]

Exempel 2

  1. Vinklarna \displaystyle -55^\circ och \displaystyle 665^\circ anger samma riktning eftersom
    \displaystyle 
     -55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}
  2. Vinklarna \displaystyle \frac{3\pi}{7} och \displaystyle -\frac{11\pi}{7} anger samma riktning eftersom
    \displaystyle 
     \frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}
  3. Vinklarna \displaystyle 36^\circ och \displaystyle 216^\circ anger inte samma riktning utan motsatta riktningar eftersom
    \displaystyle 
     36^\circ + 180^\circ = 216^\circ\,\mbox{.}


Avståndsformeln

Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter \displaystyle a och \displaystyle b, och hypotenusa \displaystyle c gäller att

Pythagoras sats:
\displaystyle c^2 = a^2 + b^2\,\mbox{.}

[Image]

Exempel 3

I triangeln till höger är
\displaystyle c^2= 3^2 + 4^2 = 9 +16 = 25

och därför är hypotenusan \displaystyle c lika med

\displaystyle c=\sqrt{25} = 5\,\mbox{.}

[Image]

Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem.

Avståndsformeln:

Avståndet \displaystyle d mellan två punkter med koordinater \displaystyle (x,y) och \displaystyle (a,b) är

\displaystyle d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}

Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna.

[Image]

Kateternas längd är lika med beloppet av skillnaden i x- och y-led mellan punkterna, dvs. \displaystyle |x-a| respektive \displaystyle |y-b|. Pythagoras sats ger sedan avståndsformeln.

Exempel 4

  1. Avståndet mellan \displaystyle (1,2) och \displaystyle (3,1) är
    \displaystyle 
     d = \sqrt{ (1-3)^2 + (2-1)^2}
   = \sqrt{(-2)^2 + 1^2}
   = \sqrt{ 4+1}
   = \sqrt{5}\,\mbox{.}
  2. Avståndet mellan \displaystyle (-1,0) och \displaystyle (-2,-5) är
    \displaystyle 
     d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2}
   = \sqrt{1^2 + 5^2}
   = \sqrt{1+25}
   = \sqrt{26}\,\mbox{.}


Cirklar

En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd \displaystyle r från en punkt \displaystyle (a,b).

[Image]


Avståndet \displaystyle r kallas för cirkelns radie och punkten \displaystyle (a,b) för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp.

[Image]

[Image]

[Image]

[Image]

Diameter Tangent Korda Sekant

[Image]

[Image]

[Image]

[Image]

Cirkelbåge Periferi Cirkelsektor Cirkelsegment

Exempel 5

En cirkelsektor är given i figuren till höger.
  1. Bestäm cirkelbågens längd.

    Medelpunktsvinkeln \displaystyle 50^\circ blir i radianer
    \displaystyle 
     50^\circ = 50 \cdot 1^\circ
          = 50 \cdot \frac{\pi}{180}\ \mbox{ radianer }
          = \frac{5\pi}{18}\ \mbox{ radianer. }

[Image]

  1. På det sätt som radianer är definierat betyder detta att cirkelbågens längd är radien multiplicerat med vinkeln mätt i radianer,
    \displaystyle 
     3 \cdot \frac{5\pi}{18}\ \mbox{ l.e. }
 = \frac{5\pi}{6}\ \mbox{ l.e. }
  1. Bestäm cirkelsektorns area.

    Cirkelsektorns andel av hela cirkeln är
    \displaystyle 
     \frac{50^\circ}{360^\circ} = \frac{5}{36}

    och det betyder att dess area är \displaystyle \frac{5}{36} delar av cirkelns area som är \displaystyle \pi r^2 = \pi 3^2 = 9\pi, dvs.

    \displaystyle 
     \frac{5}{36} \cdot 9\pi\ \mbox{ a.e. }= \frac{5\pi}{4}\ \mbox{ a.e. }

En punkt \displaystyle (x,y) ligger på cirkeln som har medelpunkt i \displaystyle (a,b) och radie \displaystyle r om dess avstånd till medelpunkten är lika med \displaystyle r. Detta villkor kan formuleras med avståndsformeln som

Cirkelns ekvation:
\displaystyle (x – a)^2 + (y – b)^2 = r^2\,\mbox{.}

[Image]

Exempel 6

  1. \displaystyle (x-1)^2 + (y-2)^2 = 9\quad är ekvationen för en cirkel med medelpunkt i \displaystyle (1,2) och radie \displaystyle \sqrt{9} = 3.

[Image]

  1. \displaystyle x^2 + (y-1)^2 = 1\quad kan skrivas som \displaystyle (x-0)^2 + (y-1)^2 = 1 och är ekvationen för en cirkel med medelpunkt i \displaystyle (0,1) och radie \displaystyle \sqrt{1} = 1.

[Image]

  1. \displaystyle (x+1)^2 + (y-3)^2 = 5\quad kan skrivas som \displaystyle (x-(-1))^2 + (y-3)^2 = 5 och är ekvationen för en cirkel med medelpunkt i \displaystyle (-1,3) och radie \displaystyle \sqrt{5} \approx 2{,}236.

[Image]

Exempel 7

  1. Ligger punkten \displaystyle (1,2) på cirkeln \displaystyle (x-4)^2 +y^2=13?

    Stoppar vi in punktens koordinater \displaystyle x=1 och \displaystyle y=2 i cirkelns ekvation har vi att
    \displaystyle \begin{align*} 
       \mbox{VL } &= (1-4)^2+2^2\\
              &= (-3)^2+2^2 = 9+4 = 13 = \mbox{HL}\,\mbox{.}
 \end{align*}

    Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln.

    [Image]

  2. Bestäm ekvationen för cirkeln som har medelpunkt i \displaystyle (3,4) och innehåller punkten \displaystyle (1,0).

    Eftersom punkten \displaystyle (1,0) ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från \displaystyle (1,0) till medelpunkten \displaystyle (3,4). Avståndsformeln ger att detta avstånd är
    \displaystyle 
     c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}

    Cirkelns ekvation är därför

    \displaystyle (x-3)^2 + (y-4)^2 = 20 \; \mbox{.}

    [Image]


Exempel 8

Bestäm medelpunkt och radie för den cirkel vars ekvation är \displaystyle \ x^2 + y^2 – 2x + 4y + 1 = 0.


Vi ska försöka skriva om cirkelns ekvation på formen

\displaystyle (x – a)^2 + (y – b)^2 = r^2

för då kan vi direkt avläsa att medelpunken är \displaystyle (a,b) och radien är \displaystyle r.

Börja med att kvadratkomplettera termerna som innehåller \displaystyle x i vänsterledet

\displaystyle 
 \underline{x^2-2x\vphantom{(}} + y^2+4y + 1
 = \underline{(x-1)^2-1^2} + y^2+4y + 1

(de understrukna termerna visar kvadratkompletteringen).

Kvadratkomplettera sedan termerna som innehåller \displaystyle y

\displaystyle 
 (x-1)^2-1^2 + \underline{y^2+4y} + 1
 = (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}

Vänsterledet är alltså lika med

\displaystyle (x-1)^2 + (y+2)^2-4

och flyttar vi över 4 till högerledet är cirkelns ekvation

\displaystyle (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}

Vi avläser att medelpunkten är \displaystyle (1,-2) och radien är \displaystyle \sqrt{4}= 2.

[Image]


Övningar

Råd för inläsning

Grund- och slutprov

Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.


Tänk på att:


Lästips

för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om:

Läs mer om Pythagoras sats på svenska Wikipedia

Läs mer i Mathworld om cirkeln


Länktips

Interaktivt experiment: sinus och cosinus i enhetscirkeln (Flash)

Den här artikeln är hämtad från http://wiki.math.se/wikis/2008/forberedandematte1/index.php/4.1_Vinklar_och_cirklar