Processing Math: Done
Lösung 2.2:3d
Aus Online Mathematik Brückenkurs 2
Wir sehen, dass die Ableitung des Nenners fast der Zähler ist
 =2x+2=2(x+1) =2x+2=2(x+1) |
Also ist das Integral
 21x2+2x+2 21x2+2x+2 (x2+2x+2) (x2+2x+2) dx. dx. |
Durch die Substitution
 x+1x2+2x+2dx= x+1x2+2x+2dx=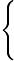 udu=x2+2x+2=(x2+2x+2) udu=x2+2x+2=(x2+2x+2) dx=2(x+1)dx dx=2(x+1)dx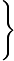 =21 =21 udu=21ln udu=21ln u u +C=21ln +C=21ln x2+2x+2 x2+2x+2 +C +C |
Hinweis: Durch die quadratische Ergänzung
sehen wir, dass
