Processing Math: Done
Lösung 2.2:4a
Aus Online Mathematik Brückenkurs 2
Unser Integral unterscheidet sich von dem in der Aufgabe nur dadurch, dass der Nenner
 dxx2+4= dxx2+4= dx4 dx4 41x2+1 41x2+1 =41 =41 dx41x2+1, dx41x2+1, |
Durch die Substitution
 dx41x2+1=41 dx41x2+1=41 dx(x dx(x 2)2+1= 2)2+1=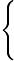 udu=x udu=x 2=21dx 2=21dx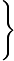 =41 =41 2duu2+1=21 2duu2+1=21 duu2+1=21arctanu+C=21arctanx2+C. duu2+1=21arctanu+C=21arctanx2+C. |
