Processing Math: Done
Lösung 3.1:4f
Aus Online Mathematik Brückenkurs 2
Nachdem 

und lösen die Gleichung für den Realteil
Die linke Seite der Gleichung wird dann
 x−1 x−1 iy+i iy+i x−i2y+i x−i2y+i x+i2y=x−iy+ix+y+ix−y=x+(2x−y)i x+i2y=x−iy+ix+y+ix−y=x+(2x−y)i |
also ist die Gleichung
Die beiden Seiten sind gleich, wenn deren Real- und Imaginärteile gleich sind, daher erhalten wir
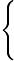 x2x−y=3 x2x−y=3 =5. =5. |
Dies ergibt  3−5=1
3−5=1
Dies überprüfen wir einfach, indem wir
 +iz=(1+i)(3−i)+i(3+i)=3−i+3i+1+3i−1=3+5i=Rechte Seite. +iz=(1+i)(3−i)+i(3+i)=3−i+3i+1+3i−1=3+5i=Rechte Seite. |
