Lösung 3.3:4b

Aus Online Mathematik Brückenkurs 2

Eine quadratische Gleichung wie diese löst man durch quadratische Ergänzung

(z−2)2−22+5(z−2)2+1=0=0

Berechnen wir die Wurzel der rechten Seite, erhalten wir die Lösungen (Wurzeln) 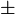z−2=i, also z=2+i und z=2−i.

Wir können diese Lösungen in der Gleichung substituieren, um zu prüfen, ob wir richtig gerechnet haben.

z=2+i:z2−4z+5z=2−i:z2−4z+5=(2+i)2−4(2+i)+5=22+4i+i2−8−4i+5=4+4i−1−8−4i+5=0=(2−i)2−4(2−i)+5=22−4i+i2−8+4i+5=4−4i−1−8+4i+5=0