Processing Math: Done
Lösung 3.3:5b
Aus Online Mathematik Brückenkurs 2
Durch quadratische Ergänzung der linken Seite erhalten wir
 z−22−i z−22−i 2− 2− 22−i 22−i 2+3−i 2+3−i z−22−i z−22−i 2− 2− 1−i+41i2 1−i+41i2 +3−i +3−i z−22−i z−22−i 2−1+i+41+3−i 2−1+i+41+3−i z−22−i z−22−i 2+49=0=0=0=0. 2+49=0=0=0=0. |
Die Wurzeln sind
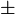 23i 23i z= z= 1+i 1+i 1−2i. 1−2i. |
Wir substituieren die Wurzeln in der ursprünglichen Gleichung
 =(1−2i)2−(2−i)(1−2i)+3−i=1−4i+4i2−(2−4i−i+2i2)+3−i=1−4i−4−2+5i+2+3−i=0.
=(1−2i)2−(2−i)(1−2i)+3−i=1−4i+4i2−(2−4i−i+2i2)+3−i=1−4i−4−2+5i+2+3−i=0.
