Lösung 3.3:5c
Aus Online Mathematik Brückenkurs 2
Wir beginnen wie immer mit quadratischer Ergänzung
 z−21+3i z−21+3i 2− 2− 21+3i 21+3i 2−4+3i 2−4+3i z−21+3i z−21+3i 2− 2− 41+23i+49i2 41+23i+49i2 −4+3i −4+3i z−21+3i z−21+3i 2−41−23i+49−4+3i 2−41−23i+49−4+3i z−21+3i z−21+3i 2−2+23i=0=0=0=0 2−2+23i=0=0=0=0 |
Lassen wir
Gleichungen wie diese löst man normalerweise mit dem Moivreschen Satz. In diesem Fall entsteht aber das Problem, das exakte Argument von der rechten Seite zu bestimmen. Auf Grund dieser Schwierigkeit lassen wir
Substituieren wir
und wir erweitern die linke Seite
Lassen wir den Real- und Imaginärteil gleich sein, erhalten wir die Gleichungen
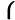 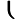 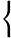 x2−y22xy=2=−23. x2−y22xy=2=−23. |
Hier könnten wir die Gleichungen direkt lösen, aber wir haben noch eine Gleichung, die wir verwenden können, nämlich
Berechnen wir den Betrag von beiden Seiten, erhalten wir
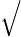 22+ 22+ −23 −23 2 2 |
also
Jetzt haben wir drei Gleichungen
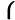 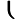 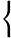           x2−y22xyx2+y2=2 x2−y22xyx2+y2=2 =−23 =−23 =25. =25. |
Addieren wir die erste Gleichung zur dritten, erhalten wir
und das ergibt 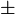 23
23
| \displaystyle {}={} | \displaystyle \tfrac{5}{2} | ||||
| \displaystyle -\ \ | \displaystyle \bigl(x^2 | \displaystyle {}-{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle 2\rlap{\bigr)} |
| \displaystyle 2y^2 | \displaystyle {}={} | \displaystyle \tfrac{1}{2} . | |||
Also ist \displaystyle y=\pm\tfrac{1}{2}. Das ergibt vier mögliche Lösungen.
| \displaystyle \left\{\begin{align}
x &= \tfrac{3}{2}\\[5pt] y &= \tfrac{1}{2} \end{align}\right. \qquad \left\{\begin{align} x &= \tfrac{3}{2}\\[5pt] y &= -\tfrac{1}{2} \end{align}\right. \qquad \left\{\begin{align} x &= -\tfrac{3}{2}\\[5pt] y &= \tfrac{1}{2} \end{align}\right. \qquad \left\{\begin{align} x &= -\tfrac{3}{2}\\[5pt] y &= -\tfrac{1}{2} \end{align}\right. |
Aber nur zwei von diesen Lösungen erfüllen die zweite Gleichung \displaystyle 2xy=-\tfrac{3}{2}, nämlich
| \displaystyle \left\{\begin{align}
x &= \tfrac{3}{2}\\[5pt] y &= -\tfrac{1}{2} \end{align}\right. \qquad\text{und}\qquad \left\{\begin{align} x &= -\tfrac{3}{2}\\[5pt] y &= \tfrac{1}{2}\,. \end{align}\right. |
Daher erhalten wir die Lösungen
| \displaystyle w=\frac{3-i}{2}\quad und \displaystyle \quad w=\frac{-3+i}{2} |
oder in \displaystyle z
| \displaystyle z=2+i\quad und \displaystyle \quad z=-1+2i\,\textrm{.} |
Wir substituieren unsere Lösungen in der ursprünglichen Gleichung, um zu kontrollieren, dass wir richtig gerechnet haben
\displaystyle \begin{align} z={}\rlap{2+i:}\phantom{-1+2i:}{}\quad z^2-(1+3i)z-4+3i &= (2+i)^2 - (1+3i)(2+i) - 4 + 3i\\[5pt] &= 4+4i+i^2-(2+i+6i+3i^2)-4+3i\\[5pt] &= 4+4i-1-2-7i+3-4+3i\\[5pt] &= 0\,,\\[10pt] z=-1+2i:\quad z^2-(1+3i)z-4+3i &= (-1+2i)^2-(1+3i)(-1+2i)-4+3i\\[5pt] &= (-1)^2-4i+4i^2-(-1+2i-3i+6i^2)-4+3i\\[5pt] &= 1-4i-4+1+i+6-4+3i\\[5pt] &= 0\,\textrm{.} \end{align}
