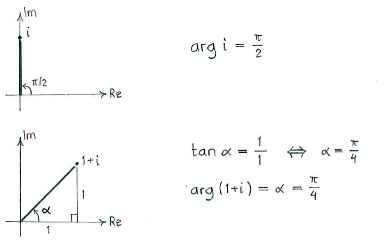Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 3.2:5d

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
When dividing two complex numbers, the numerator's magnitude is divided by the denominator's absolute value and the numerator's argument is subtracted from the numerator's argument.
+
When dividing two complex numbers, the numerator's magnitude is divided by the denominator's magnitude and the numerator's argument is subtracted from the numerator's argument.
-
The argument of the quotient
+
The argument of the quotient <math>i/(1+i)</math> is therefore
-
<math>\frac{i}{1+i}</math>
+
-
is therefore
+
 +
{{Displayed math||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.}</math>}}
-
<math>\arg \frac{i}{1+i}=\arg i-\arg \left( 1+i \right)</math>
+
We obtain the argument of <math>i</math> and <math>1+i</math> by drawing the numbers in the complex plane and using a little trigonometry.
-
 
+
-
 
+
-
We obtain the argument of
+
-
<math>i</math>
+
-
and
+
-
<math>\text{1}+i</math>
+
-
by drawing the numbers in the complex plane and using a little trigonometry:
+
-
 
+
[[Image:3_2_5_d.gif|center]]
[[Image:3_2_5_d.gif|center]]
- 
Hence, we obtain
Hence, we obtain
-
 
+
{{Displayed math||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.}</math>}}
-
<math>\arg \frac{i}{1+i}=\arg i-\arg \left( 1+i \right)=\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}</math>
+

Version vom 12:43, 29. Okt. 2008

When dividing two complex numbers, the numerator's magnitude is divided by the denominator's magnitude and the numerator's argument is subtracted from the numerator's argument.

The argument of the quotient i(1+i) is therefore

argi1+i=argi−arg(1+i).

We obtain the argument of i and 1+i by drawing the numbers in the complex plane and using a little trigonometry.

Hence, we obtain

argi1+i=argi−arg(1+i)=2−4=4.
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:5d“