Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 1.1:4

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
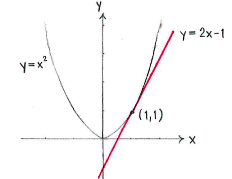
If we write the equation of the tangent as
If we write the equation of the tangent as
-
{{Displayed math||<math>y=kx+m</math>}}
+
{{Abgesetzte Formel||<math>y=kx+m</math>}}
we know that the tangent's slope ''k'' is equal to the derivative of <math>y = x^2</math> at the point <math>x=1\,</math>, and since <math>y^{\,\prime} = 2x\,</math>, so
we know that the tangent's slope ''k'' is equal to the derivative of <math>y = x^2</math> at the point <math>x=1\,</math>, and since <math>y^{\,\prime} = 2x\,</math>, so
-
{{Displayed math||<math>k = y^{\,\prime}(1) = 2\cdot 1 = 2\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>k = y^{\,\prime}(1) = 2\cdot 1 = 2\,\textrm{.}</math>}}
We can determine the constant ''m'' with the condition that the tangent should go through the grazing point (1,1), i.e. the point (1,1) should satisfy the equation of the tangent
We can determine the constant ''m'' with the condition that the tangent should go through the grazing point (1,1), i.e. the point (1,1) should satisfy the equation of the tangent
-
{{Displayed math||<math>1 = 2\cdot 1 + m</math>}}
+
{{Abgesetzte Formel||<math>1 = 2\cdot 1 + m</math>}}
which gives that <math>m=-1</math>.
which gives that <math>m=-1</math>.
Zeile 19: Zeile 19:
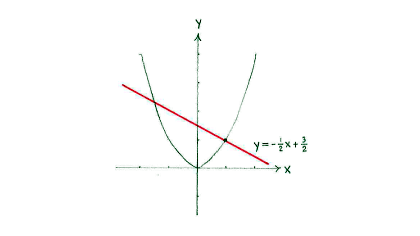
Because two straight lines which are perpendicular to each other have slopes which satisfy <math>k_{1}\cdot k_{2} = -1\,</math>, the normal must have a slope which is equal to
Because two straight lines which are perpendicular to each other have slopes which satisfy <math>k_{1}\cdot k_{2} = -1\,</math>, the normal must have a slope which is equal to
-
{{Displayed math||<math>-\frac{1}{k} = -\frac{1}{2}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>-\frac{1}{k} = -\frac{1}{2}\,\textrm{.}</math>}}
The equation of the normal can therefore be written as
The equation of the normal can therefore be written as
-
{{Displayed math||<math>y=-\frac{1}{2}x+n</math>}}
+
{{Abgesetzte Formel||<math>y=-\frac{1}{2}x+n</math>}}
where ''n'' is some constant.
where ''n'' is some constant.
Zeile 29: Zeile 29:
Since the normal must pass through the line (1,1), we can determine the constant ''n'' if we substitute the point into the equation of the normal,
Since the normal must pass through the line (1,1), we can determine the constant ''n'' if we substitute the point into the equation of the normal,
-
{{Displayed math||<math>1=-\frac{1}{2}\cdot + n</math>}}
+
{{Abgesetzte Formel||<math>1=-\frac{1}{2}\cdot + n</math>}}
and this gives <math>n=\tfrac{3}{2}\,</math>.
and this gives <math>n=\tfrac{3}{2}\,</math>.
[[Image:1_1_4-3(3).gif|center]]
[[Image:1_1_4-3(3).gif|center]]

Version vom 12:51, 10. Mär. 2009

If we write the equation of the tangent as

y=kx+m

we know that the tangent's slope k is equal to the derivative of y=x2 at the point x=1, and since y=2x, so

k=y(1)=21=2.

We can determine the constant m with the condition that the tangent should go through the grazing point (1,1), i.e. the point (1,1) should satisfy the equation of the tangent

1=21+m

which gives that m=−1.

The normal to the curve y=x2 at the point (1,1) is the straight line which is perpendicular to the tangent at the same point.

Because two straight lines which are perpendicular to each other have slopes which satisfy k1k2=−1, the normal must have a slope which is equal to

−k1=−21.

The equation of the normal can therefore be written as

y=−21x+n

where n is some constant.

Since the normal must pass through the line (1,1), we can determine the constant n if we substitute the point into the equation of the normal,

1=−21+n

and this gives n=23.

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.1:4“