Processing Math: 100%
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 1.1:5

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
Suppose that the tangent touches the curve at the point <math>(x_0,y_0)</math>. That point must, first and foremost, lie on the curve and therefore satisfy the equation of the curve, i.e.
Suppose that the tangent touches the curve at the point <math>(x_0,y_0)</math>. That point must, first and foremost, lie on the curve and therefore satisfy the equation of the curve, i.e.
-
{{Displayed math||<math>y_0 = -x_0^2\,\textrm{.}</math>|(1)}}
+
{{Abgesetzte Formel||<math>y_0 = -x_0^2\,\textrm{.}</math>|(1)}}
If we now write the equation of the tangent as <math>y=kx+m</math>, the slope of the tangent, ''k'', is given by the value of the curve's derivative, <math>y^{\,\prime} = -2x</math>, at <math>x=x_0</math>,
If we now write the equation of the tangent as <math>y=kx+m</math>, the slope of the tangent, ''k'', is given by the value of the curve's derivative, <math>y^{\,\prime} = -2x</math>, at <math>x=x_0</math>,
-
{{Displayed math||<math>k = -2x_0\,\textrm{.}</math>|(2)}}
+
{{Abgesetzte Formel||<math>k = -2x_0\,\textrm{.}</math>|(2)}}
The condition that the tangent goes through the point <math>(x_0,y_0)</math> gives us that
The condition that the tangent goes through the point <math>(x_0,y_0)</math> gives us that
-
{{Displayed math||<math>y_{0} = k\cdot x_0 + m\,\textrm{.}</math>|(3)}}
+
{{Abgesetzte Formel||<math>y_{0} = k\cdot x_0 + m\,\textrm{.}</math>|(3)}}
In addition to this, the tangent should also pass through the point (1,1),
In addition to this, the tangent should also pass through the point (1,1),
-
{{Displayed math||<math>1 = k\cdot 1 + m\,\textrm{.}</math>|(4)}}
+
{{Abgesetzte Formel||<math>1 = k\cdot 1 + m\,\textrm{.}</math>|(4)}}
Equations (1)-(4) constitute a system of equations in the unknowns <math>x_0</math>, <math>y_{0}</math>, <math>k</math> and <math>m</math>.
Equations (1)-(4) constitute a system of equations in the unknowns <math>x_0</math>, <math>y_{0}</math>, <math>k</math> and <math>m</math>.
Zeile 21: Zeile 21:
Equation (2) gives that <math>k = -2 x_0</math> and substituting this into equation (4) gives
Equation (2) gives that <math>k = -2 x_0</math> and substituting this into equation (4) gives
-
{{Displayed math||<math>1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.}</math>}}
With ''k'' and ''m'' expressed in terms of <math>x_0</math> and <math>y_0</math>, (3) becomes an equation that is expressed completely in terms of <math>x_0</math>
With ''k'' and ''m'' expressed in terms of <math>x_0</math> and <math>y_0</math>, (3) becomes an equation that is expressed completely in terms of <math>x_0</math>
and <math>y_0</math>,
and <math>y_0</math>,
-
{{Displayed math||<math>y_0 = -2x_0^2 + 2x_0 + 1\,\textrm{.}</math>|(3')}}
+
{{Abgesetzte Formel||<math>y_0 = -2x_0^2 + 2x_0 + 1\,\textrm{.}</math>|(3')}}
This equation, together with (1), is a system of equations in <math>x_0</math> and <math>y_0</math>,
This equation, together with (1), is a system of equations in <math>x_0</math> and <math>y_0</math>,
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
y_{0} &= -x_0^{2}\,,\\[5pt]
y_{0} &= -x_0^{2}\,,\\[5pt]
y_{0} &= -2x_0^2 + 2x_0 + 1\,\textrm{.}
y_{0} &= -2x_0^2 + 2x_0 + 1\,\textrm{.}
Zeile 37: Zeile 37:
Substituting equation (1) into (3') gives us an equation in <math>x_0</math>,
Substituting equation (1) into (3') gives us an equation in <math>x_0</math>,
-
{{Displayed math||<math>-x_0^2 = -2x_0^2 + 2x_0 + 1\,,</math>}}
+
{{Abgesetzte Formel||<math>-x_0^2 = -2x_0^2 + 2x_0 + 1\,,</math>}}
i.e.
i.e.
-
{{Displayed math||<math>x_0^2 - 2x_0 - 1 = 0\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x_0^2 - 2x_0 - 1 = 0\,\textrm{.}</math>}}
This quadratic equation has solutions
This quadratic equation has solutions
-
{{Displayed math||<math>x_0 = 1-\sqrt{2}\qquad\text{and}\qquad x_0 = 1+\sqrt{2}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x_0 = 1-\sqrt{2}\qquad\text{and}\qquad x_0 = 1+\sqrt{2}\,\textrm{.}</math>}}
Equation (1) gives the corresponding y-values,
Equation (1) gives the corresponding y-values,
-
{{Displayed math||<math>y_0 = -3+2\sqrt{2}\qquad\text{and}\qquad y_0 = -3-2\sqrt{2}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>y_0 = -3+2\sqrt{2}\qquad\text{and}\qquad y_0 = -3-2\sqrt{2}\,\textrm{.}</math>}}
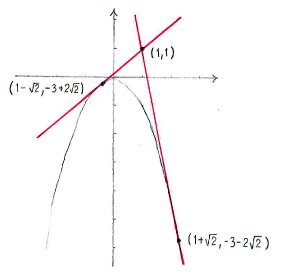
Thus, the answers are the points <math>(1-\sqrt{2},-3+2\sqrt{2})</math> and
Thus, the answers are the points <math>(1-\sqrt{2},-3+2\sqrt{2})</math> and

Version vom 12:51, 10. Mär. 2009

Suppose that the tangent touches the curve at the point (x0y0). That point must, first and foremost, lie on the curve and therefore satisfy the equation of the curve, i.e.

y0=−x20. (1)

If we now write the equation of the tangent as y=kx+m, the slope of the tangent, k, is given by the value of the curve's derivative, y=−2x, at x=x0,

k=−2x0. (2)

The condition that the tangent goes through the point (x0y0) gives us that

y0=kx0+m. (3)

In addition to this, the tangent should also pass through the point (1,1),

1=k1+m. (4)

Equations (1)-(4) constitute a system of equations in the unknowns x0, y0, k and m.

Because we are looking for x0 and y0, the first step is to try and eliminate k and m from the equations.

Equation (2) gives that k=−2x0 and substituting this into equation (4) gives

1=−2x0+mm=2x0+1.

With k and m expressed in terms of x0 and y0, (3) becomes an equation that is expressed completely in terms of x0 and y0,

y0=−2x20+2x0+1. (3')

This equation, together with (1), is a system of equations in x0 and y0,

y0y0=−x20=−2x20+2x0+1.

Substituting equation (1) into (3') gives us an equation in x0,

−x20=−2x20+2x0+1

i.e.

x20−2x0−1=0.

This quadratic equation has solutions

x0=1−2andx0=1+2. 

Equation (1) gives the corresponding y-values,

y0=−3+22andy0=−3−22. 

Thus, the answers are the points (1−2−3+22)  and (1+2−3−22) .

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.1:5“