Lösung 1.3:2c
Aus Online Mathematik Brückenkurs 2
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 9: | Zeile 9: | ||
As regards item 1, we set the derivative equal to zero and obtain the equation | As regards item 1, we set the derivative equal to zero and obtain the equation | ||
| - | {{ | + | {{Abgesetzte Formel||<math>f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}</math>}} |
Dividing both sides by 6 and completing the square, we obtain | Dividing both sides by 6 and completing the square, we obtain | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}</math>}} |
This gives us the equation | This gives us the equation | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}</math>}} |
and taking the square root gives the solutions | and taking the square root gives the solutions | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
x &= -\frac{1}{2}-\sqrt{\frac{9}{4}} = -\frac{1}{2}-\frac{3}{2} = -2\,,\\[5pt] | x &= -\frac{1}{2}-\sqrt{\frac{9}{4}} = -\frac{1}{2}-\frac{3}{2} = -2\,,\\[5pt] | ||
x &= -\frac{1}{2}+\sqrt{\frac{9}{4}} = -\frac{1}{2}+\frac{3}{2} = 1\,\textrm{.} | x &= -\frac{1}{2}+\sqrt{\frac{9}{4}} = -\frac{1}{2}+\frac{3}{2} = 1\,\textrm{.} | ||
Version vom 12:55, 10. Mär. 2009
There are three types of points at which the function can have local extreme points,
- critical points, i.e. where \displaystyle f^{\,\prime}(x)=0,
- points where the function is not differentiable, and
- endpoints of the interval of definition.
Because our function is a polynomial, it is defined and differentiable everywhere, and therefore does not have any points which satisfy items 2 and 3.
As regards item 1, we set the derivative equal to zero and obtain the equation
| \displaystyle f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.} |
Dividing both sides by 6 and completing the square, we obtain
| \displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.} |
This gives us the equation
| \displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4} |
and taking the square root gives the solutions
| \displaystyle \begin{align}
x &= -\frac{1}{2}-\sqrt{\frac{9}{4}} = -\frac{1}{2}-\frac{3}{2} = -2\,,\\[5pt] x &= -\frac{1}{2}+\sqrt{\frac{9}{4}} = -\frac{1}{2}+\frac{3}{2} = 1\,\textrm{.} \end{align} |
This means that if the function has several extreme points, they must be among \displaystyle x=-2 and \displaystyle x=1.
Then, we write down a sign table for the derivative, and read off the possible extreme points.
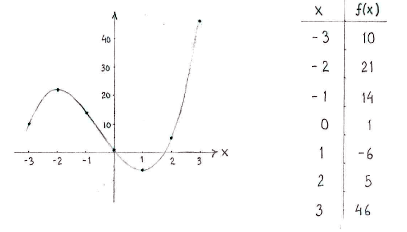
| \displaystyle x | \displaystyle -2 | \displaystyle 1 | |||
| \displaystyle f^{\,\prime}(x) | \displaystyle + | \displaystyle 0 | \displaystyle - | \displaystyle 0 | \displaystyle + |
| \displaystyle f(x) | \displaystyle \nearrow | \displaystyle 21 | \displaystyle \searrow | \displaystyle -6 | \displaystyle \nearrow |
The function has a local maximum at \displaystyle x=-2 and a local minimum at \displaystyle x=1.
We obtain the overall appearance of the graph of the function from the table and by calculating the value of the function at a few points.