Lösung 1.3:5
Aus Online Mathematik Brückenkurs 2
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 9: | Zeile 9: | ||
The area of the cross-section is | The area of the cross-section is | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
A(\alpha) &= 10\cdot 10\cos\alpha + 2\cdot\frac{1}{2}\cdot 10\cos\alpha \cdot 10\sin\alpha\\[5pt] | A(\alpha) &= 10\cdot 10\cos\alpha + 2\cdot\frac{1}{2}\cdot 10\cos\alpha \cdot 10\sin\alpha\\[5pt] | ||
&= 100\cos \alpha (1+\sin\alpha)\,\textrm{.} | &= 100\cos \alpha (1+\sin\alpha)\,\textrm{.} | ||
| Zeile 23: | Zeile 23: | ||
We differentiate the area function: | We differentiate the area function: | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
A'(\alpha) &= 100\cdot (-\sin\alpha)\cdot (1+\sin\alpha) + 100\cdot\cos\alpha \cdot \cos\alpha\\[5pt] | A'(\alpha) &= 100\cdot (-\sin\alpha)\cdot (1+\sin\alpha) + 100\cdot\cos\alpha \cdot \cos\alpha\\[5pt] | ||
&= -100\sin\alpha - 100\sin^2\!\alpha + 100\cos^2\!\alpha\,\textrm{.} | &= -100\sin\alpha - 100\sin^2\!\alpha + 100\cos^2\!\alpha\,\textrm{.} | ||
| Zeile 30: | Zeile 30: | ||
At a critical point <math>A'(\alpha)=0</math> and this gives us the equation | At a critical point <math>A'(\alpha)=0</math> and this gives us the equation | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\sin\alpha + \sin^2\!\alpha - \cos^2\!\alpha = 0</math>}} |
after eliminating the factor -100. We replace <math>\cos^2\!\alpha</math> with <math>1-\sin^2\!\alpha</math> (according to the Pythagorean identity) to obtain an equation solely in <math>\sin\alpha\,</math>, | after eliminating the factor -100. We replace <math>\cos^2\!\alpha</math> with <math>1-\sin^2\!\alpha</math> (according to the Pythagorean identity) to obtain an equation solely in <math>\sin\alpha\,</math>, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
\sin\alpha + \sin^2\!\alpha - (1-\sin^2\!\alpha) &= 0\\[5pt] | \sin\alpha + \sin^2\!\alpha - (1-\sin^2\!\alpha) &= 0\\[5pt] | ||
2\sin^2\!\alpha + \sin\alpha - 1 &= 0\,\textrm{.} | 2\sin^2\!\alpha + \sin\alpha - 1 &= 0\,\textrm{.} | ||
| Zeile 41: | Zeile 41: | ||
This is a second-degree equation in <math>\sin\alpha</math> and completing the square gives that | This is a second-degree equation in <math>\sin\alpha</math> and completing the square gives that | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
2\bigl(\sin\alpha + \tfrac{1}{4}\bigr)^{2} - 2\bigl(\tfrac{1}{4}\bigr)^2 - 1 &= 0\\[5pt] | 2\bigl(\sin\alpha + \tfrac{1}{4}\bigr)^{2} - 2\bigl(\tfrac{1}{4}\bigr)^2 - 1 &= 0\\[5pt] | ||
\bigl(\sin\alpha + \tfrac{1}{4}\bigr)^2 &= \frac{9}{16} | \bigl(\sin\alpha + \tfrac{1}{4}\bigr)^2 &= \frac{9}{16} | ||
| Zeile 53: | Zeile 53: | ||
If we summarize, we know therefore that the cross-sectional area has local minimum points at <math>\alpha = 0</math> and <math>\alpha = \pi/2</math> and that we have a critical point at <math>\alpha = \pi/6\,</math>. This critical point must be a maximum, which we can also show using the second derivative, | If we summarize, we know therefore that the cross-sectional area has local minimum points at <math>\alpha = 0</math> and <math>\alpha = \pi/2</math> and that we have a critical point at <math>\alpha = \pi/6\,</math>. This critical point must be a maximum, which we can also show using the second derivative, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
A''(\alpha) &= -100\cos\alpha - 100\cdot 2\sin\alpha\cdot\cos\alpha + 100\cdot 2\cos\alpha \cdot (-\sin\alpha)\\[5pt] | A''(\alpha) &= -100\cos\alpha - 100\cdot 2\sin\alpha\cdot\cos\alpha + 100\cdot 2\cos\alpha \cdot (-\sin\alpha)\\[5pt] | ||
&= -100\cos\alpha (1+4\sin\alpha)\,, | &= -100\cos\alpha (1+4\sin\alpha)\,, | ||
| Zeile 60: | Zeile 60: | ||
which is negative at <math>\alpha = \pi/6</math>, | which is negative at <math>\alpha = \pi/6</math>, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
A''(\pi/6) &= -100\cos\frac{\pi}{6}\cdot \Bigl(1+4\sin\frac{\pi}{6}\Bigr)\\[5pt] | A''(\pi/6) &= -100\cos\frac{\pi}{6}\cdot \Bigl(1+4\sin\frac{\pi}{6}\Bigr)\\[5pt] | ||
&= -100\cdot\frac{\sqrt{3}}{2}\cdot \Bigl( 1+4\cdot \frac{1}{2} \Bigr)<0\,\textrm{.} | &= -100\cdot\frac{\sqrt{3}}{2}\cdot \Bigl( 1+4\cdot \frac{1}{2} \Bigr)<0\,\textrm{.} | ||
Version vom 12:56, 10. Mär. 2009
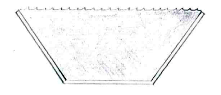
The channel holds most water when its cross-sectional area is greatest.
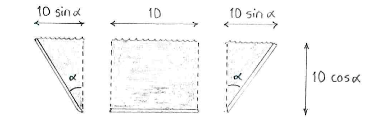
By dividing up the channel's cross-section into a rectangle and two triangles we can, with the help of a little trigonometry, determine the lengths of the rectangle's and triangles' sides, and thence the cross-sectional area.
The area of the cross-section is
 )=10 10cos+22110cos10sin=100cos(1+sin). |
If we limit the angle to lie between 
2
- Maximise the function
A( when)=100cos(1+sin)
- Maximise the function
2
The area function is a differentiable function and the area is least when =0=2
We differentiate the area function:
 ()=100(−sin)(1+sin)+100coscos=−100sin−100sin2+100cos2. |
At a critical point ()=0
| +sin2−cos2=0 |
after eliminating the factor -100. We replace
| +sin2−(1−sin2)2sin2+sin−1=0=0. |
This is a second-degree equation in
 sin+41 2−2412−1sin+412=0=916 |
and we obtain =−41
43=−1=21
The case =−12=21=6=6
If we summarize, we know therefore that the cross-sectional area has local minimum points at =0=2=6
()=−100cos−1002sincos+1002cos(−sin)=−100cos(1+4sin) |
which is negative at =6
(6)=−100cos6 1+4sin6 =−1002 31+421 0. |
There are no local maximum points other than =6
