Processing Math: Done
Lösung 3.2:6f
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 17: | Zeile 17: | ||
The whole expression becomes | The whole expression becomes | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
\frac{(2+2i)(1+i\sqrt{3}\,)}{3i(\sqrt{12}-2i)} | \frac{(2+2i)(1+i\sqrt{3}\,)}{3i(\sqrt{12}-2i)} | ||
&= \frac{2\sqrt{2}\Bigl(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\Bigr)\cdot 2\Bigl( \cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\Bigr)}{3\Bigl(\cos\dfrac{\pi}{2}+i\sin \dfrac{\pi}{2}\Bigr)\cdot 4\Bigl(\cos\Bigl(-\dfrac{\pi}{6}\Bigr)+i\sin\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)}\\[5pt] | &= \frac{2\sqrt{2}\Bigl(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\Bigr)\cdot 2\Bigl( \cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\Bigr)}{3\Bigl(\cos\dfrac{\pi}{2}+i\sin \dfrac{\pi}{2}\Bigr)\cdot 4\Bigl(\cos\Bigl(-\dfrac{\pi}{6}\Bigr)+i\sin\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)}\\[5pt] | ||
Version vom 13:10, 10. Mär. 2009
We can write every factor in the numerator and denominator in polar form and then use the arithmetical rules for multiplication and division in polar form:
r1(cos 
+isin)
r2(cos
+isin)=r1r2
cos(+)+isin(+)
r2(cos +isin)r1(cos+isin)=r2r1cos(−)+isin(−).
In fact, most of the work consists of writing all the factors in polar form:
| 
|
| 
|
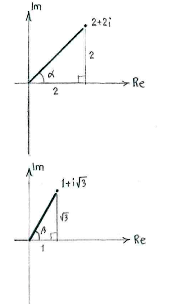
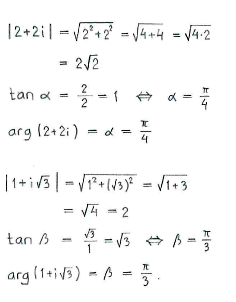
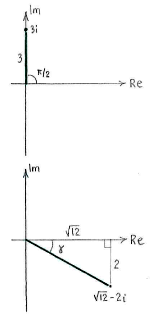
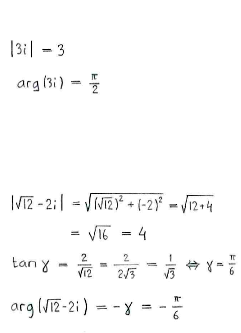
The whole expression becomes
 12−2i)(2+2i)(1+i3)=22 cos 4+isin4 2cos3+isin33cos2+isin24cos−6+isin−6=12cos2−6+isin2−642cos4+3+isin4+3=12cos3+isin342cos127+isin127=1242cos127−3+isin127−3=32cos4+isin4. |
