Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 3.3:1a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
Powers are repeated multiplications and because multiplication is a relatively simple arithmetical operation when it is carried out in polar form, calculating powers also becomes fairly simple in polar form,
Powers are repeated multiplications and because multiplication is a relatively simple arithmetical operation when it is carried out in polar form, calculating powers also becomes fairly simple in polar form,
-
{{Displayed math||<math>\bigl(r(\cos\alpha + i\sin\alpha)\bigr)^n = r^n(\cos n\alpha + i\sin n\alpha)\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>\bigl(r(\cos\alpha + i\sin\alpha)\bigr)^n = r^n(\cos n\alpha + i\sin n\alpha)\,\textrm{.}</math>}}
The equation above is called de Moivre's formula.
The equation above is called de Moivre's formula.
Zeile 11: Zeile 11:
Using the calculations above, we see that
Using the calculations above, we see that
-
{{Displayed math||<math>1+i = \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4} \Bigr)\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>1+i = \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4} \Bigr)\,\textrm{.}</math>}}
De Moivre's formula now gives
De Moivre's formula now gives
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
(1+i)^{12}
(1+i)^{12}
&= \bigl(\sqrt{2}\,\bigr)^{12}\Bigl(\cos \Bigl(12\cdot\frac{\pi}{4}\Bigr) + i\sin \Bigl(12\cdot\frac{\pi}{4}\Bigr)\Bigr)\\[5pt]
&= \bigl(\sqrt{2}\,\bigr)^{12}\Bigl(\cos \Bigl(12\cdot\frac{\pi}{4}\Bigr) + i\sin \Bigl(12\cdot\frac{\pi}{4}\Bigr)\Bigr)\\[5pt]

Version vom 13:10, 10. Mär. 2009

Powers are repeated multiplications and because multiplication is a relatively simple arithmetical operation when it is carried out in polar form, calculating powers also becomes fairly simple in polar form,

r(cos+isin)n=rn(cosn+isinn). 

The equation above is called de Moivre's formula.

The plan is therefore to rewrite 1+i in polar form, raise the expression to the power 12 using de Moivre's formula and then to write the answer in the form a+ib.

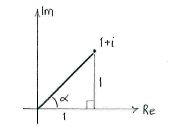
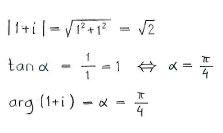
Image:3_3_1_a1.gif Image:3_3_1_a_text.gif

Using the calculations above, we see that

1+i=2cos4+isin4. 

De Moivre's formula now gives

(1+i)12=212cos124+isin124=2(12)12cos3+isin3=26(−1+i0)=64(−1)=−64.
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:1a“