Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 2.1:4b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
K (Solution 2.1:4b moved to Lösung 2.1:4b: Robot: moved page)

Version vom 10:18, 11. Mär. 2009

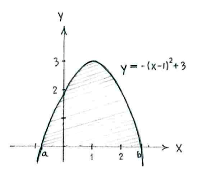
By completing the square of the equation of the curve

y=−x2+2x+2=−x2−2x−2=−(x−1)2−12−2=−(x−1)2+3

we can read off that the curve is a downward parabola with maximum value y=3 when x=1.

The region whose area we shall determine is the one shaded in the figure.

We can express this area using the integral

Area=ba−x2+2x+2dx 

where a and b are the x-coordinates for the points of intersection between the parabola and the x-axis.

A solution plan is to first determine the intersection points, x=a and x=b, and then calculate the area using the integral formula above.

The parabola cuts the x-axis when its y-coordinate is zero, i.e.

0=−x2+2x+2

and because we have already completed the square of the right-hand side once, the equation can be written as

0=−(x−1)2+3

or

(x−1)2=3.

Taking the square root gives x=13 . The points of intersection are x=1−3  and x=1+3 .

The area we are looking for is therefore given by

Area=1+31−3−x2+2x+2dx. 

Instead of directly starting to calculate, we can start from the integrand in the form we obtain after completing its square,

Area=1+31−3−(x−1)2+3dx 

which seems easier. Because the expression x−1 inside the square is a linear expression, we can write down a primitive function “in the usual way”,

Area= −3(x−1)3+3x 1+31−3. 

(If one is uncertain of this step, it is possible to differentiate the primitive function and see that one really does get the integrand back). Hence,

Area=−3(1+3−1)3+3(1+3)−−3(1−3−1)3+3(1−3)=−3(3)3+3+33+3(−3)3−3+33=−3333+33+3(−3)(−3)(−3)+33=−333+33−333+33=−3+33−3+33=(−1+3−1+3)3=43.


Note: The calculations become a lot more complicated if one starts from

1+31−3−x2+2x+2dx= 
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:4b“