Processing Math: Done

Aus Online Mathematik Brückenkurs 2

Version vom 12:59, 10. Mär. 2009 (bearbeiten) Tekbot (Diskussion | Beiträge) K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) ← Zum vorherigen Versionsunterschied

Version vom 10:18, 11. Mär. 2009 (bearbeiten) (rückgängig) Tekbot (Diskussion | Beiträge) K (Solution 2.1:4c moved to Lösung 2.1:4c: Robot: moved page) Zum nächsten Versionsunterschied →

---

Version vom 10:18, 11. Mär. 2009

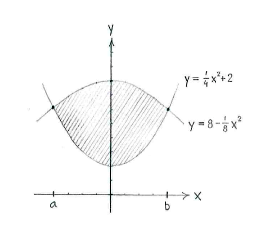
First, we need a picture of what the region looks like.

Both curves, y=x24+2 and y=8−x28, are parabolas, the first with a minimum value y=2 when x=0, and the second with a maximum value of y=8 when x=0. Roughly speaking, the curves have the appearance shown in the figure below, where the shaded region whose area we are trying to find lies between the curves.

The region is bounded above by the parabola y=8−x28 and below by the parabola y=x24+2. If we can determine the x-coordinates, x=a and x=b, for the points of intersection between the curves, the area we are looking for will be given by

Area=ba8−81x2−41x2+2dx.

The integrand is the y-value for the upper parabola minus the corresponding y-value for the lower parabola.

At the points where the curves intersect each other, the x- and y-coordinates are equal, which gives the equation system,

yy=8−81x2=41x2+2.

If we eliminate y from this system, we get the following equation for x,

8−81x2=41x2+2.

If we move the x2-terms onto one side and the constants onto the other, we obtain

41x2+81x2=8−2

i.e.

41+81x283x2x2=6=6=16.

The x-coordinates of the points of intersection are therefore equal to x=−4 and x=4.

The area of the area between the curves is given by

Area=4−48−81x2−41x2+2dx=4−48−81x2−41x2−2dx=4−46−81+41x2dx=4−46−83x2dx= 6x−833x3 4−4= 6x−8x3 4−4=64−843−6(−4)−8(−4)3=24−8+24−8=32.