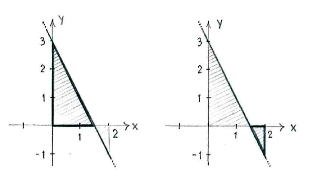Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 2.1:1c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Zeile 9: Zeile 9:
Wenn wir das Integral berechen, müssen wir berücksichtigen dass die Fläche die unter der ''y''-Achse liegt, von der Fläche oberhalb der ''y''-Achse subtrahiert werden muss.
Wenn wir das Integral berechen, müssen wir berücksichtigen dass die Fläche die unter der ''y''-Achse liegt, von der Fläche oberhalb der ''y''-Achse subtrahiert werden muss.
-
Wir teilen unsere Fläche also auf
+
Wir teilen unsere Fläche also in eine linke und eine rechte Fläche auf,
[[Image:2_1_1_c2.gif|center]]
[[Image:2_1_1_c2.gif|center]]

Version vom 16:09, 28. Apr. 2009

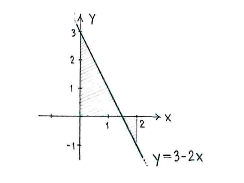
Die Gerade y=3−2x schneidet die x-Achse im Punkt

y=3−2x=0x=32

Also liegt ein Teil der Geraden x=32 unter der y-Achse.

Wenn wir das Integral berechen, müssen wir berücksichtigen dass die Fläche die unter der y-Achse liegt, von der Fläche oberhalb der y-Achse subtrahiert werden muss.

Wir teilen unsere Fläche also in eine linke und eine rechte Fläche auf,

und erhalten

20(3−2x)dx=21233−21211=49−41=2. 
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1c“