Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 2.1:1b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 2.1:1b moved to Solution 2.1:1b: Robot: moved page)
Aktuelle Version (07:33, 21. Aug. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 5 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
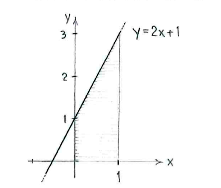
Die Funktion <math>y=2x+1</math> ist eine Gerade, die die ''y''-Achse in <math>y=1</math> schneidet und die Steigung 2 hat.
-
<center> [[Image:2_1_1b-1(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
-
{{NAVCONTENT_START}}
+
-
<center> [[Image:2_1_1b-2(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+
 +
Das Integral entspricht der Fläche unter der Geraden zwischen <math>x=0</math>
 +
und <math>x=1</math>.
[[Image:2_1_1_b1.gif|center]]
[[Image:2_1_1_b1.gif|center]]
 +
 +
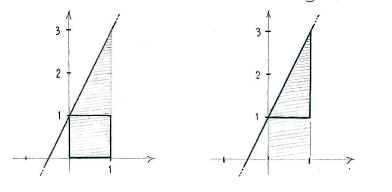
Wir teilen die Fläche in zwei Teilflächen auf, ein Rechteck und ein Dreieck
 +
[[Image:2_1_1_b2.gif|center]]
[[Image:2_1_1_b2.gif|center]]
 +
 +
und addieren deren Flächen, um die gesamte Fläche zu bekommen.
 +
 +
Das Integral ist daher
 +
 +
{{Abgesetzte Formel||<math>\begin{align}
 +
\int\limits_{0}^{1} (2x+1)\,dx
 +
&= \text{(Fläche des Rechtecks)} + \text{(Fläche des Dreiecks)}\\
 +
&= 1\cdot 1 + \frac{1}{2}\cdot 1\cdot 2 = 2\,\textrm{.}
 +
\end{align}</math>}}

Aktuelle Version

Die Funktion y=2x+1 ist eine Gerade, die die y-Achse in y=1 schneidet und die Steigung 2 hat.

Das Integral entspricht der Fläche unter der Geraden zwischen x=0 und x=1.

Wir teilen die Fläche in zwei Teilflächen auf, ein Rechteck und ein Dreieck

und addieren deren Flächen, um die gesamte Fläche zu bekommen.

Das Integral ist daher

10(2x+1)dx=(Fläche des Rechtecks)+(Fläche des Dreiecks)=11+2112=2.
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1b“