3.3:2c alternativ exp
Aus Online Mathematik Brückenkurs 2
K (Robot: Automated text replacement (-ü +ü)) |
K (Robot: Automated text replacement (-ö +ö)) |
||
| (Der Versionsvergleich bezieht eine dazwischen liegende Version mit ein.) | |||
| Zeile 41: | Zeile 41: | ||
5. <math>n=4</math> : <math>z=2^{\frac{1}{10}}\, e^{i \frac{37\pi}{20} \pi}</math> | 5. <math>n=4</math> : <math>z=2^{\frac{1}{10}}\, e^{i \frac{37\pi}{20} \pi}</math> | ||
| - | Die | + | Die nächste Lösung für <math> n=5 </math> ist wegen der 2-<math>\pi</math> Periodizität identisch mit der 1. Lösung mit <math> n=0 </math>. |
Aktuelle Version
Wir stellen
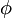 +isin +isin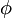 )=rei )=rei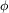 |
wobei r = Betrag und 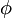
 −1−i −1−i = =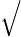 (−1)2+(−1)2= (−1)2+(−1)2= 2 2 |
Dann klammern wir  2
2
 2(−2 2(−2 2−2 2−2 2i) 2i) |
Gesucht werden alle Winkel 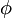
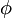 =2− =2− 2 2 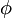 =2− =2− 2 2 |
Diese Winkel sind
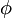 = = 4+ 4+ +2n +2n =45 =45 +2n +2n |
mit 
Also
 2ei(45 2ei(45 +2n +2n ) ) |
Wir ziehen die 5. Wurzel, um
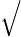 5 5 2ei(45 2ei(45 +2n +2n )=221 )=221 51ei51(45 51ei51(45 +2n +2n )=2110ei( )=2110ei( 4+52n 4+52n ) ) |
Die Gleichung
1. \displaystyle n=0 : \displaystyle z=2^{\frac{1}{10}} \, e^{i \frac{1}{4} \pi} (falls es schlecht zu lesen ist: 2 hoch \displaystyle \frac{1}{10} mal e hoch \displaystyle i \frac{1}{4} \pi )
2. \displaystyle n=1 : \displaystyle z=2^{\frac{1}{10}}\, e^{i \frac{13}{20} \pi}
3. \displaystyle n=2 : \displaystyle z=2^{\frac{1}{10}}\, e^{i \frac{21}{20} \pi}
4. \displaystyle n=3 : \displaystyle z=2^{\frac{1}{10}}\, e^{i \frac{29}{20} \pi}
5. \displaystyle n=4 : \displaystyle z=2^{\frac{1}{10}}\, e^{i \frac{37\pi}{20} \pi}
Die nächste Lösung für \displaystyle n=5 ist wegen der 2-\displaystyle \pi Periodizität identisch mit der 1. Lösung mit \displaystyle n=0 .
