Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 1.1:1a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Robot: Automated text replacement (-[[Bild: +[[Image:))
Zeile 1: Zeile 1:
{{NAVCONTENT_START}}
{{NAVCONTENT_START}}
 +
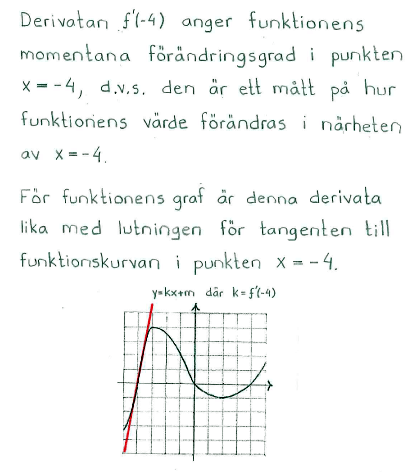
The derivative f'(-4)gives the function's instantaneous rate of change at the point x=-4, i.e. it is a measure of the function's value changes in the vicinity of x=-4.
 +
 +
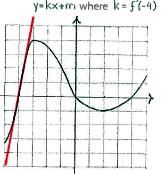
In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point x=-4.
 +
 +
[[Image:1_1_1_a1.gif|center]]
 +
 +
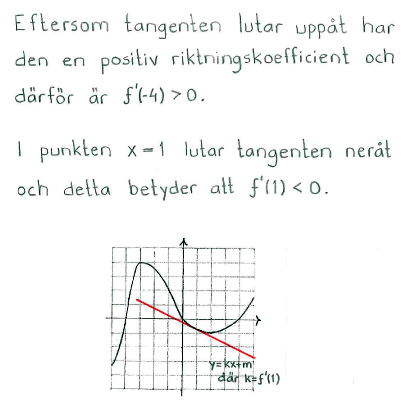
Because the tangent is sloping upwards, it has a positive gradient and therefore f'(-4)>0.
 +
 +
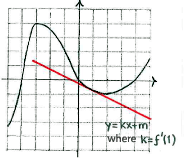
At the point x=1, the tangent slopes downwards and this means that f'(1)<0.
 +
 +
[[Image:1_1_1_a2.gif|center]]
 +
 +
<center> [[Image:1_1_1a-1(2).gif]] </center>
<center> [[Image:1_1_1a-1(2).gif]] </center>
{{NAVCONTENT_STOP}}
{{NAVCONTENT_STOP}}
Zeile 5: Zeile 18:
<center> [[Image:2_1_1a-2(2).gif]] </center>
<center> [[Image:2_1_1a-2(2).gif]] </center>
{{NAVCONTENT_STOP}}
{{NAVCONTENT_STOP}}
- 
-
[[Image:1_1_1_a1.gif|center]]
 
- 
-
[[Image:1_1_1_a2.gif|center]]
 

Version vom 15:24, 5. Sep. 2008

The derivative f'(-4)gives the function's instantaneous rate of change at the point x=-4, i.e. it is a measure of the function's value changes in the vicinity of x=-4.

In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point x=-4.

Because the tangent is sloping upwards, it has a positive gradient and therefore f'(-4)>0.

At the point x=1, the tangent slopes downwards and this means that f'(1)<0.


Image:1_1_1a-1(2).gif
Image:2_1_1a-2(2).gif
Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.1:1a“