Lösung 2.1:1b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 2.1:1b moved to Solution 2.1:1b: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
The graph of the function
-
<center> [[Image:2_1_1b-1(2).gif]] </center>
+
<math>y=2x+1</math>
-
{{NAVCONTENT_STOP}}
+
is a straight line which cuts the
-
{{NAVCONTENT_START}}
+
<math>y</math>
-
<center> [[Image:2_1_1b-2(2).gif]] </center>
+
-axis at
-
{{NAVCONTENT_STOP}}
+
<math>y=\text{1}</math>
 +
and has gradient
 +
<math>2</math>.
 +
 
 +
The integral's value is the area under the straight line and between
 +
<math>x=0\text{ }</math>
 +
and
 +
<math>x=\text{1}</math>.
 +
 
[[Image:2_1_1_b1.gif|center]]
[[Image:2_1_1_b1.gif|center]]
 +
 +
We can divide up the region under the graph into a square and rectangle,
 +
 +
[[Image:2_1_1_b2.gif|center]]
[[Image:2_1_1_b2.gif|center]]
 +
 +
and then add up the area to obtain the total area.
 +
 +
The value of the integral is
 +
 +
 +
<math>\int\limits_{0}^{1}{\left( 2x+1 \right)\,}dx=</math>
 +
(area of the square) + (area of the triangle)
 +
<math>1\centerdot 1+\frac{1}{2}\centerdot 1\centerdot 2=2</math>

Version vom 11:37, 17. Okt. 2008

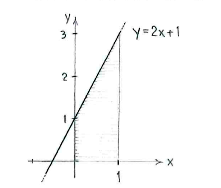
The graph of the function \displaystyle y=2x+1 is a straight line which cuts the \displaystyle y -axis at \displaystyle y=\text{1} and has gradient \displaystyle 2.

The integral's value is the area under the straight line and between \displaystyle x=0\text{ } and \displaystyle x=\text{1}.


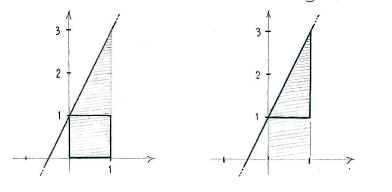
We can divide up the region under the graph into a square and rectangle,


and then add up the area to obtain the total area.

The value of the integral is


\displaystyle \int\limits_{0}^{1}{\left( 2x+1 \right)\,}dx= (area of the square) + (area of the triangle) \displaystyle 1\centerdot 1+\frac{1}{2}\centerdot 1\centerdot 2=2

Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1b“