Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 3.3:2a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 3.3:2a moved to Solution 3.3:2a: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
An equation of the type “
-
<center> [[Image:3_3_2a-1(2).gif]] </center>
+
<math>z^{n}</math>
-
{{NAVCONTENT_STOP}}
+
= a complex number” is called a binomial equation and these are usually solved by going over to polar form and using de Moivre's formula.
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Image:3_3_2a-2(2).gif]] </center>
+
We start by writing
-
{{NAVCONTENT_STOP}}
+
<math>z\text{ }</math>
 +
and
 +
<math>\text{1}</math>
 +
in polar form
 +
 
 +
 
 +
<math>\begin{align}
 +
& z=r\left( \cos \alpha +i\sin \alpha \right) \\
 +
& 1=1\left( \cos 0+i\sin 0 \right) \\
 +
\end{align}</math>
 +
 
 +
 
 +
The equation then becomes
 +
 
 +
 
 +
<math>r^{4}\left( \cos 4\alpha +i\sin 4\alpha \right)=1\left( \cos 0+i\sin 0 \right)</math>
 +
 
 +
 
 +
where we have used de Moivre's formula on the left-hand side. In order that both sides are equal, they must have the same magnitude and the same argument to within a multiple of
 +
<math>2\pi </math>, i.e.
 +
 
 +
 
 +
<math>\left\{ \begin{array}{*{35}l}
 +
r^{4}=1 \\
 +
4\alpha =0+2n\pi \quad \left( n\text{ an arbitrary integer} \right)\text{ } \\
 +
\end{array} \right.</math>
 +
 +
This means that
 +
 
 +
 
 +
<math>\left\{ \begin{array}{*{35}l}
 +
r=1 \\
 +
\alpha =\frac{n\pi }{2}\quad \left( n\text{ an arbitrary integer} \right)\text{ } \\
 +
\end{array} \right.</math>
 +
 
 +
The solutions are thus (in polar form)
 +
 
 +
 
 +
<math>z=1\centerdot \left( \cos \frac{n\pi }{2}+i\sin \frac{n\pi }{2} \right)</math>, for
 +
<math>n=0,\ \pm 1,\ \pm 2,...</math>
 +
 
 +
 
 +
but observe that the argument on the right-hand side essentially takes only four different values
 +
<math>0,\ {\pi }/{2}\;,\ \pi </math>
 +
and
 +
<math>{3\pi }/{2}\;</math>, because other values of
 +
<math>n\text{ }</math>
 +
give some of these values plus/minus a multiple of
 +
<math>2\pi </math>.
 +
 
 +
The equation's solutions are therefore
 +
 
 +
 
 +
<math>z=\left\{ \begin{array}{*{35}l}
 +
1\centerdot \left( \cos 0+i\sin 0 \right) \\
 +
1\centerdot \left( \cos {\pi }/{2}\;+i\sin {\pi }/{2}\; \right) \\
 +
1\centerdot \left( \cos \pi +i\sin \pi \right) \\
 +
1\centerdot \left( \cos {3\pi }/{2}\;+i\sin {3\pi }/{2}\; \right) \\
 +
\end{array} \right.=\left\{ \begin{matrix}
 +
1 \\
 +
i \\
 +
-1 \\
 +
-i \\
 +
\end{matrix} \right.</math>
 +
 
 +
 
 +
NOTE: note that if we mark these solutions on the complex number plane, we see that they are corners in a regular quadrilateral.
 +
 
[[Image:3_3_2_a.gif|center]]
[[Image:3_3_2_a.gif|center]]

Version vom 09:04, 24. Okt. 2008

An equation of the type “ zn = a complex number” is called a binomial equation and these are usually solved by going over to polar form and using de Moivre's formula.

We start by writing z and 1 in polar form


z=rcos+isin1=1cos0+isin0 


The equation then becomes


r4cos4+isin4=1cos0+isin0 


where we have used de Moivre's formula on the left-hand side. In order that both sides are equal, they must have the same magnitude and the same argument to within a multiple of 2, i.e.


r4=14=0+2nn an arbitrary integer  

This means that


r=1=2nn an arbitrary integer  

The solutions are thus (in polar form)


z=1cos2n+isin2n , for n=0 1 2


but observe that the argument on the right-hand side essentially takes only four different values 0 2  and 32, because other values of n give some of these values plus/minus a multiple of 2.

The equation's solutions are therefore


z=1cos0+isin01cos2+isin21cos+isin1cos32+isin32=1i−1−i


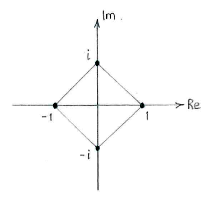
NOTE: note that if we mark these solutions on the complex number plane, we see that they are corners in a regular quadrilateral.


Von „http://wiki.math.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:2a“